CryptoCTF 2024 medium 分类 团队解题 writeup 之三

这次 medium 分类题量还是最多的，结果一开始里面很多题都不可解，甚至比赛结束了还 TMD 有一道零解。

我去年买了个表

Melek

题目描述

给定素数 $p$。在 $GF(p)$ 下定义 $t$ 次多项式

$$f(x) = \sum_{i=0}^{n-1}a_i x^{i}$$

其中 $a_0 = c = m^e \bmod p$，$e$ 已知。然后随机生成 $GF(p)$ 下 $t$ 个数 $x_1, x_2, \ldots, x_t$，并求出 $f(x_1), f(x_2), \ldots, f(x_t)$。已知 $(x_i, f(x_i)), i = 1, 2, \ldots, t$，求 $m$。

我的解答

这一看就是 Shamir’s Secret Sharing，其背后的原理是拉格朗日插值定理，这里可以直接以矩阵的视角求出系数即可：

from Crypto.Util.number import *

with open('output.txt', 'r') as f:
    exec(f.read())

def solve(enc):
    e, p, PT = enc
    t = len(PT)
    A = [[pow(PT[i][0], j, p) for j in range(t)] for i in range(t)]
    b = [PT[i][1] for i in range(t)]
    A = matrix(Zmod(p), A)
    b = vector(Zmod(p), b)
    x = A.solve_right(b)
    cc = x[0]
    print(f'{cc = }')
    print(f'{e = }')
    print(f'{p = }')

solve(enc)

解得 $c$ 之后，再去解 $m$，这里发现 $\gcd(e, p-1) \ne 1$，其实等于 $2$，那就先解掉 $e/g$ 的部分，再开平方就行了：

from Crypto.Util.number import *

cc = 
e = 
p = 
g = gcd(e, p-1)
print(f'{g = }')
d0 = inverse(e // g, p-1)
m0 = pow(cc, d0, p)
m = Zmod(p)(m0).sqrt()
print(long_to_bytes(int(m)))

得到 flag 为：

CCTF{SSS_iZ_4n_3fF!ciEn7_5ecr3T_ShArIn9_alGorItHm!}

Nabat

题目描述

首先产生一个随机的 $n$，多项式 $g(x) = x^2+x+2$，我们需要输入一个整系数多项式 $f$，使得 $f$ 满足：

1. $f$ 的系数绝对值均不大于 1
2. $f$ 的次数 $d_f$ 满足 $d_f + 1 \ge 2 \log(n)$
3. $f$ 中系数为 0 的项的个数不小于 $\lfloor 2 d_f / 3 \rfloor - 3$
4. $g \mid f - n$

我的解答

感觉第一点和第四点比较直接，第二点和第三点相反比较抽象。

我们可以反向出发：我们可以从 $-n$ 开始，利用等式关系 $2 = -x^2 - x$ 生成高次的项！

如果 $n$ 是奇数的话，这样会没法完全利用等式关系生成高次的项。我们 尽可能地利用等式关系生成高次的项，直至 $n$ 剩到 1 或者-1 就停止

譬如 $n=3$，我们就有

$$3 \equiv 1 + 2 \equiv 1 - x - x^2 \pmod{g}$$

这样我们可以满足第四点，然后还需要满足第三点。这个就需要在第 $i$ 步的时候就需要同时照顾到第 $i+1$ 步的系数，使第 $i+1$ 步的系数尽量能凑成偶数（在下一步中能产生系数为 0 的项）。还是上面那个例子，我们就会更倾向于下面的消法：

$$3 \equiv -1 + 4 \equiv -1 - 2(x - x^2) \pmod{g}$$

这样 $2x$ 就会在下一步消成 $0$，就能在期望上满足第三个条件（看成一个马尔可夫过程）：

• $p(下一步消成0|这一步消不成0) = 1$
• $p(下一步消成0|这一步消成0) = 1/2$
• $\mathbb{E}(消成0的步数) = p(这一步消成0) + 2p(这一步消不成0)p(下一步消成0|这一步消不成0) = 3/2$
• $\mathbb{E}(p(消成0)) = 1/\mathbb{E}(消成0的步数) = 2/3$

代码如下：

from pwn import *
import re

context.proxy = socks.SOCKS5, '172.24.144.1', 7890
context.log_level = 'debug'

class Gao:
    def __init__(self):
        # self.conn = process(['sage', 'another.sage'])
        self.conn = remote('02.cr.yp.toc.tf', '37771')
        self.patt = r'n = (.*?),'
    
    def gao_1(self):
        self.conn.recvuntil('Your are in')
        s = self.conn.recvline().decode()
        m = re.search(self.patt, s)
        n = ZZ(m.group(1))
        k = 4396
        clist = [0] * k
        clist[0] = n
        for i in range(k - 2):
            t = clist[i] // 2
            if clist[i] % 2 == 1 and (t + clist[i+1]) % 2 == 1:
                t += 1
            clist[i] -= 2 * t
            clist[i+1] -= t
            clist[i+2] -= t
        PR.<x> = PolynomialRing(ZZ)
        f = PR(clist)
        self.conn.sendline(str(f))

    def gao(self):
        for i in range(11):
            print(f'{i = }')
            self.gao_1()
        self.conn.interactive()

if __name__ == '__main__':
    g = Gao()
    g.gao()

flag 为：

CCTF{0p71M!5TiC_rEpR3SenT4t!0n_Of_n_8Y_Frobenius!}

---

赛后反思

一开始第三个条件为

• $f$ 中系数为 0 的项的个数不小于 $\lfloor 2 d_f / 3 \rfloor$

并且要 check 40 组才算过。这个约束还是太强了，上面的算法很大概率会挂……

我他妈想问问这个出题的哈麻批，$n=11$ 的时候你他妈给老子出一组解出来？

一九九七的队友都是用格做的，一开始还不明白，后来一想确实，因为是对多个目标同时进行最小化，所以应该是用格更加科学。

所以用多项式系数的视角，不难看出有以下格：

$$\begin{bmatrix}1 & k_0 & k_1 & \ldots & k_{d-2} \end{bmatrix}\begin{bmatrix}1 & n & 0 & 0 & 0 & \ldots & 0 \\ 0 & 2 & 1 & 1 & 0 & \ldots & 0 \\ 0 & 0 & 2 & 1 & 1 & \ldots & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & 0 & 0 & \ldots & 1 \end{bmatrix}=\begin{bmatrix}1 & c_0 & c_1 & \ldots c_d \end{bmatrix}$$

其中 $c_i$ 为 $f$ 的第 $i$ 次项系数。代码如下：

from pwn import context, process, remote, socks
import re

context.proxy = socks.SOCKS5, '172.24.144.1', 7890
context.log_level = 'debug'

class Gao:
    def __init__(self):
        self.conn = process(['sage', 'another.sage'])
        # self.conn = remote('02.cr.yp.toc.tf', '37771')
        self.patt = r'n = (.*?),'
    
    def check(self, f, l):
        print(f'Trying {f}')
        coefs = f.list()
        _b1 = all(abs(_) <= 1 for _ in coefs)
        _b2 = f.degree() + 1 - 2 * n(log(l)) >= 0
        _b3 = coefs.count(0) >= 2 * f.degree() // 3 - 3
        print(f'{coefs.count(0) = }')
        print(f'{2 * f.degree() // 3 - 3 = }')
        return _b1 and _b2 and _b3

    def gao_1(self):
        self.conn.recvuntil('Your are in')
        s = self.conn.recvline().decode()
        m = re.search(self.patt, s)
        n = ZZ(m.group(1))
        # Need to be adjusted
        d = 120
        M = [[0 for j in range(d+2)] for i in range(d)]
        M[0][0] = 1
        M[0][1] = n
        for i in range(d-1):
            M[i+1][i+1] = 2
            M[i+1][i+2] = 1
            M[i+1][i+3] = 1
        M = matrix(ZZ, M)
        # v = M.LLL()
        v = M.BKZ(block_size=16)
        PR.<x> = PolynomialRing(ZZ)
        for vline in v:
            if vline[0] < 0:
                vline = -vline
            if vline[0] == 1:
                f = PR(vline[1:].list())
                if self.check(f, n):
                    print(f'AOLIGEI!!! {n = }')
                    self.conn.sendline(str(f))
                    break
        else:
            raise Exception(f'GG {n = }')

    def gao(self):
        for i in range(39):
            print(f'{i = }')
            self.gao_1()
        self.conn.interactive()

if __name__ == '__main__':
    g = Gao()
    g.gao()

确实这样做会科学一点，但是这样做仍然未去显式优化题目的第三个条件（只能最多求求系数的和之类的，系数的绝对值之和都难做到），题目的第三个条件仍然比较难满足，而且对于某些 $n$，就算削弱之后的条件三都满足不了（无解），譬如 $n = 1764196894$，如果有解的话欢迎交流。

Nazdone

题目描述

有 未知 参数 $m, a, z$。素数 $p, q, r$ 满足如下形式（以 $p$ 为例）：

$$p = \sum_{i=1}^{z_0} m^{r_{i}} + 1$$

其中 $z_0 \le z$ 为一个随机数，$1 \le r_i < a$。

有 $n = pqr$，$e = m^3 + z - 2$，$c = m_0^e \bmod n$。

已知 $n, c$，求 $m_0$。

我的解答

因为 $p, q, r$ 均具有那个在 $m$ 进制下的表示稀疏的形式，所以 $n$ 在 $m$ 进制下的表示应该系数不会太大。

譬如：

$$(a^3 + a^2 + 1)(a^5 + a^4 + 1) = a^8 + 2a^7 + a^6 + a^5 + a^4 + a^3 + a^2 + 1$$

右边的系数都是比较小的，这个“小”的刻画可以用和来表示。

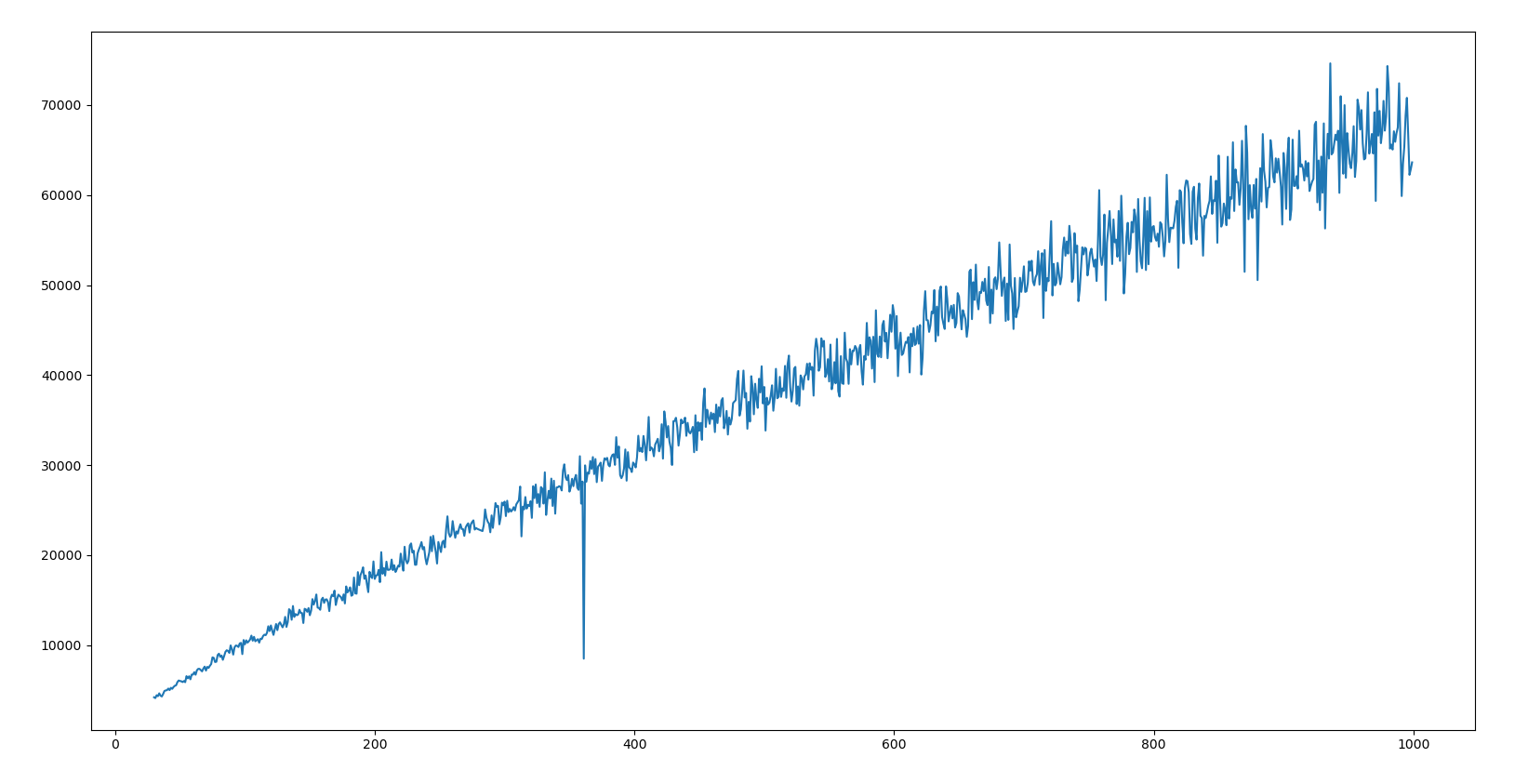
我们可以枚举一下 $m$，把 $n$ 在 $m$ 进制下表示的系数和做一个统计，画一个图看看有没有极小值存在：

from matplotlib import pyplot as plt

n = 
c = 
print(f'{n.bit_length() = }')

def get_base(n, m):
    bases = []
    while n != 0:
        bases.append(n % m)
        n //= m
    return bases

mrange = range(30, 1000)
sbases = []
for m in mrange:
    bases = get_base(n, m)
    sbases.append(sum(bases))
plt.plot(mrange, sbases)
plt.show()

# Filter out small numbers
mrange = mrange[200:]
sbases = sbases[200:]
sm = list(zip(sbases, mrange))
sm.sort()
print(sm[:20])

然后就发现有一个突变：

这个突变对应的 $m=361$ 应该就是我们需要的结果。

但是呢，将 $n$ 转换为 $m$ 进制下的多项式，发现首项系数不为 1：

$$19 x^{160} + x^{153} + x^{151} + x^{148} + x^{146} + 38 x^{143} + \ldots$$

正当我还在纳闷为啥的时候，V 告诉我正确的 $m$ 应该是 19

卧槽，V！英雄登场！

确实，因为 $m$ 开根号就是 19，而且这些不为 1 的系数也是 19 的倍数，更加佐证了这一点。

所以最后就是将 $n$ 写成 $m$ 进制下的多项式之后，就可以进行多项式的因式分解。然后把 $m$ 代入到因式里面就是 $n$ 的素因数（这个套路在 强网拟态 2022 里面出现过）：

n = 
c = 

m = 19

def get_base(n, m):
    bases = []
    while n != 0:
        bases.append(n % m)
        n //= m
    return bases

PR.<x> = PolynomialRing(ZZ)
f = PR(get_base(n, m))
print(f)
p = factor(f)
for pi, ai in p:
    print(pi(m))

然后就是朴实无华的解密。这里要注意一下，$m$ 的值是已知的，但是 $z$ 的值是未知的，应该不会太大，需要枚举。然后我们莽猜一波 $e$ 跟 $\phi(n)$ 互素：

from Crypto.Util.number import *

p = 
q = 
r = 

n = 
c = 

assert n == p*q*r

m = 19
for z in range(3, 30):
    try:
        e = m ** 3 + z - 2
        d = inverse(e, (p-1)*(q-1)*(r-1))
        mm = pow(c, d, n)
        print(long_to_bytes(mm))
    except:
        pass

得到 flag 为：

CCTF{nUmb3r5_1N_D!fFerEn7_8As35_4r3_n!cE!?}