CryptoCTF 2024 easy 分类团队解题 writeup

这次 easy 分类比赛的时候我当时看了一道 MD5 的，结果感觉很谜语，就没去仔细看了。要懂得把球传给队友

那么赛后就复盘一下

Alibos

题目描述

私钥 $s_k$ 为 $d_s$ 位十进制数，公钥 $p_k$ 可被写成如下形式：

$p_k = \lfloor 10^{d_s} \left( \sqrt{s_k} - \lfloor \sqrt{s_k} \rfloor \right) \rfloor$

记 $p_k$ 为 $d_p$ 位十进制数

加密算法：

在 $m$ 的十进制表示中在右边加上很多个 1，使其成为 $d_p$ 位十进制数；
计算 $c = \left( p_k + d_p^2 m \right) \bmod 10^{d_p}$

给出 $p_k$ 和 $c$，试求 $m$。

我的解答

首先可以求出 $d_p$ 的值，然后直接求出 $m$ 的值即可：

$m = \left( c - p_k \right) d_p^{-2} \bmod 10^{d_p}$

代码如下：

from Crypto.Util.number import *

pkey = 8582435512564229286688465405009040056856016872134514945016805951785759509953023638490767572236748566493023965794194297026085882082781147026501124183913218900918532638964014591302221504335115379744625749001902791287122243760312557423006862735120339132655680911213722073949690947638446354528576541717311700749946777
enc  = 6314597738211377086770535291073179315279171595861180001679392971498929017818237394074266448467963648845725270238638741470530326527225591470945568628357663345362977083408459035746665948779559824189070193446347235731566688204757001867451307179564783577100125355658166518394135392082890798973020986161756145194380336

d_p = len(str(pkey))
m = (enc - pkey) * inverse(d_p**2, 10**d_p) % 10**d_p
for i in range(d_p):
    print(f'#{i}: {long_to_bytes(m // 10**i)}')

得到 flag 为：

1	CCTF{h0M3_m4De_cRyp70_5ySTeM_1N_CryptoCTF!!!}

Beheaded

题目描述

题目给了一个加密的 shell 脚本，以及一个加密后的文件。

注意运行题目所给定的 shell 脚本需要使用 imagemagick 7 版本，6 版本会报错，详见：

https://askubuntu.com/questions/1315603/where-is-the-magick-command-of-imagemagick

然后 apt install imagemagick 好像默认安装的是 6 版本的，很烦，可以通过这里的安装步骤安装 imagemagick 7

首先题目在一个 ppm 文件里面画了一个 flag，然后将这个 ppm 文件的前 3 行丢掉，最后把剩下的内容用一个密钥，以 AES-256 ECB 的方式进行加密。

然后注意最后的加密命令是追加写，但是密钥内容不会变。

我的解答

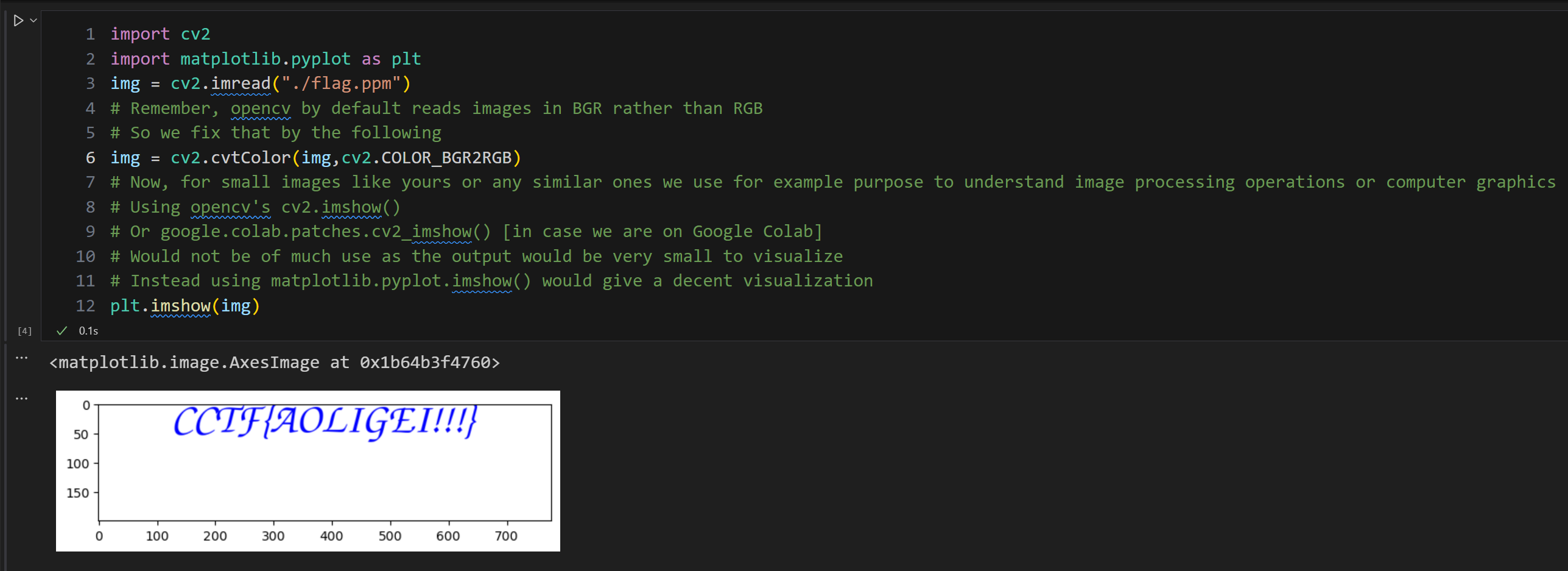
ppm 文件的构成形式可以参考这里。譬如在一个 X=777, Y=200 的画布上画上 CCTF{AOLIGEI!!!}，那么画出来的东西大概长这样：

然后注意到是 AES-256 的 block_size 是 16，加上加密方式为 ECB，所以应该是通过密文块内容反推回明文块的内容。只是说我们需要更多地了解一下 ppm 的文件格式：

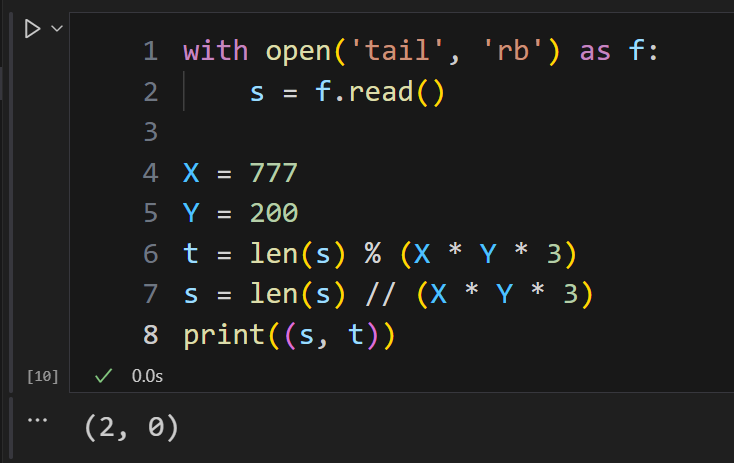
所以应该是 bitmap 存储，只不过这里用 2 字节来表示一个灰度值。

这样的话，我们有理由相信，密文块频数最高的块是背景颜色加密之后的结果！所以我们就做一个简易的二分类：统计密文块的频数，最高频数的密文块就认为其对应明文为背景，其他密文块就认为其对应明文为前景。

然后有个坑点，因为加密的命令是追加写，所以可能有同样大小、不同内容的加密块垛在一起，所以可能需要先枚举有多少个加密快，然后根据这个去得到密文块可能的大小。其中密文块的大小为：

将 3 2 X * Y pad 成 16 的倍数
3 为图像通道数（RGB 图像为 3）
2 为位深度（题目中的位深度为 65536，也就是一个灰度值占 2 个字节）
X 和 Y 分别就是宽高

所以枚举的策略就是：

先枚举有多少个图像（即多少个加密块，必为文件大小的约数）
再枚举密文大小（即 3 2 X * Y）的值
枚举高 Y（必为密文大小的约数）

代码如下（因为没有用 sagemath，所以获得因数那里实现比较土味）：

from collections import Counter
import cv2

filename = '../all_flags.enc'
with open(filename, 'rb') as f:
    s = f.read()

BLOCK_SIZE = 16

def get_blocks(s):
    return [s[BLOCK_SIZE*i:BLOCK_SIZE*(i+1)] for i in range(len(s) // BLOCK_SIZE)]

cblocks = get_blocks(s)
probably_white = Counter(cblocks).most_common(1)[0][0]

MBLOCKS = b''.join([b'\xFF' * BLOCK_SIZE if cblock == probably_white else b'\x00' * BLOCK_SIZE \
                    for cblock in cblocks])

def get_real_size_list(size):
    real_size_list = []
    for SIZE_OFFSET in range(BLOCK_SIZE):
        real_size = size - SIZE_OFFSET - 1
        if (real_size % 6 == 0):
            real_size_list.append(real_size)
    return real_size_list

def get_factors(x, L, R):
    results = []
    t = L
    while t * t <= x and t <= R:
        if x % t == 0:
            results.append(t)
        t += 1
    return results

for num_pics in get_factors(len(s), 1, 100):
    one_pic_size = len(s) // num_pics
    for pic_id in range(num_pics):
        for real_size in get_real_size_list(one_pic_size):
            for Y in get_factors(real_size // 6, 100, 500):
                X = real_size // (6 * Y)
                PPM_HEAD = f'P6\n{X} {Y}\n65535\n'
                PPM_BYTES = PPM_HEAD.encode() + MBLOCKS[pic_id*one_pic_size:(pic_id+1)*one_pic_size]
                PPM_FILENAME = f'results/ppm/{real_size}_{Y}_{pic_id}.ppm'
                PNG_FILENAME = f'results/png/{real_size}_{Y}_{pic_id}.png'
                print(f'PNG: {PNG_FILENAME}, {one_pic_size = }, {len(PPM_BYTES) = }, {num_pics = }')
                with open(PPM_FILENAME, 'wb') as f:
                    f.write(PPM_BYTES)
                img = cv2.imread(PPM_FILENAME)
                cv2.imwrite(PNG_FILENAME, img)

枚举一下，然后看生成出的图像是否有文字，结果还真就发现了一组 2288430_235_0.png：

耐心点翻一下这一组的结果，发现 2288430_235_16.png 就包含 flag：

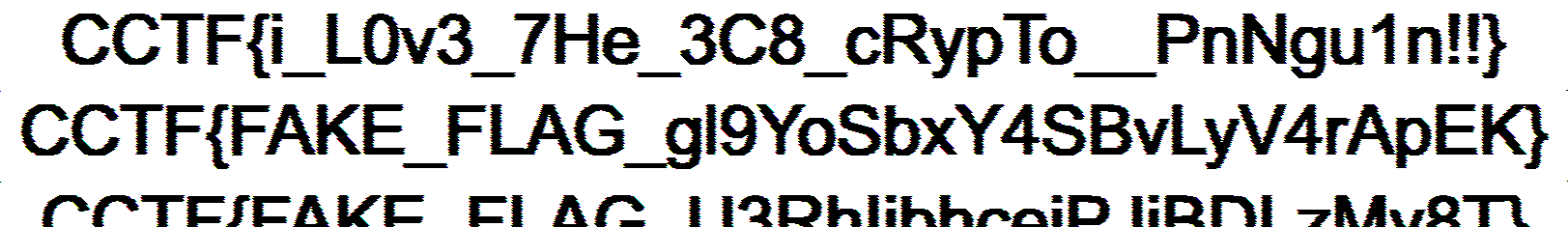
得到 flag 为：

1	CCTF{i_L0v3_7He_3C8_cRypTo__PnNgu1n!!}

Mashy

题目描述

需要提供 8 组 bytes 对 (x1, x2)，使得：

md5(hex(x1) xor hex(x2)) 不为 ae09d7510659ca40eda3e45ca70e9606
md5(x1) xor md5(x2) xor md5(salt) 为 a483b30944cbf762d4a3afc154aad825

其中 salt 为一个未知固定值。

我的解答

当时反查了一下这两个 md5 值的原像，发现：

ae09d7510659ca40eda3e45ca70e9606 查不出
a483b30944cbf762d4a3afc154aad825 为 emelinjulca

这里要点名批评一下 cmd5，下面那条记录居然 tmd 要付费，劳资在看这道题目的时候是黑曼巴时间凌晨 4 点，试问这个时候你家会员找哪里去借？最后还是去了 crackstation，结果一下子就破开了，日

然后未央居然跟我说第一个的原像是 b'\x00' * 256，我嘞个雷啊，怎么试出来的啊……anyway，第一个好像不重要，主要是第二个，他奶奶的这个 salt 的值又不知道是啥，这不硬猜？

好在又是未央，莽猜了一波 salt 的值就是那个 md5 值的原像 emelinjulca，那是真的牛皮啊，这出题的脑子是不是被驴踢了？你要是问什么哈希长度扩展攻击的话这种值不告诉也就算了，这尼玛币不告诉让猜，多少沾点闹弹了。这波啊，这波未央立血吗天功！

未央：看到那么多个 solve，往简单的方向猜（

所以这粑粑题实际上也就变成了：提供 8 组 bytes 对 (x1, x2)，使得：

hex(x1) xor hex(x2) 不为 b'\x00' * 256
md5(x1) 等于 md5(x2)

那这不就是碰撞出 8 对 bytes 使得值不相等且 md5 值相等，直接 fastcoll 一把梭拉几把倒了，出题人快点滚回家玩儿蛋去吧。

至于 fastcoll 的使用：

先生成一个前缀：echo "caonima" > pref.txt
然后运行 ⑨ 次：./md5_fastcoll pref.txt
就可以得到 ⑨ 组共同以 caonima 开头的碰撞对了

然后提交代码如下：

from pwn import *
import os


class Gao:
    def __init__(self) -> None:
        self.conn = remote('01.cr.yp.toc.tf', '13771')
        self.path = '/mnt/d/Tools/hashclash-static-release-v1.2b/bin'
    
    def gao_1(self, i):
        part_1_path = os.path.join(self.path, f'pref_msg1_{i+1}.txt')
        part_2_path = os.path.join(self.path, f'pref_msg2_{i+1}.txt')
        with open(part_1_path, 'rb') as f:
            part_1 = f.read()
        with open(part_2_path, 'rb') as f:
            part_2 = f.read()
        self.conn.sendline(part_1.hex())
        self.conn.sendline(part_2.hex())
    
    def gao(self):
        for i in range(8):
            self.gao_1(i)
        self.conn.interactive()

if __name__ == '__main__':
    g = Gao()
    g.gao()

得到 flag 为：

1	CCTF{mD5_h4Sh_cOlL!Si0N_CrYp7o_ch41lEnGe!!!}