这次 medium 分类题量是最多的，内容方面是最丰富的，两极分化比较严重。

有脑筋急转弯的，有考察 SageMath API 使用的，有 MISC 题目混进来的……

总之 medium 分类最难的比 tough 还要更难……

Roldy

题目描述

题目的加密基于 ECB 模式的分组加密，以及基于 pyope 包中的 OPE 加密算法。

与远程终端交互，可以知道 flag 的密文，也能进行任意次输入明文，得到加密结果的操作。

试求 flag。

我的解答

首先搜一波 OPE 是什么：

https://crypto.stackexchange.com/questions/37375/order-preserving-encryption-ope-and-leakage

简单来说，OPE 就是 Order-Preserving Encryption（保序加密）的缩写。

接着具体看到 pyope 包的页面：

https://pypi.org/project/pyope/

其中有：

1
assert cipher.encrypt(1000) < cipher.encrypt(2000) < cipher.encrypt(3000)

也就是说，该加密函数是单调递增的。

那么就很简单了：可以根据该加密函数单调递增的性质，对明文进行二分，然后根据密文的值是否不小于目标值来决定选哪个子区间。

然后需要注意的一个点：我在实战的时候把输入限定到了可见字符，因为它是要求直接输明文的。这就导致我当时撸了一个类似“向下对齐”的函数。因为我就怕二分的时候分到了一个字符串里面带回车之类的，然后服务器读的时候就把后面的内容给截断了。（实际上好像并没有什么必要？）

然后还有就是服务器在实际操作的时候不是辣么的稳定。有的时候二分分着分着就会突然连接断开。这个时候，我们需要把每一块的至今的二分结果（子区间）存下来。这样，我们就能在下次 run 脚本的时候，恢复之前的子区间，继续二分。

最后就是最后一块有可能不满 16bytes，那么就需要在“向下对齐”的函数里面限定，特殊处理一下。如果观察到 block_size=16 的时候，二分查找分不出来，那么就改 block_size 为 15……不过，好像它 flag 设计的就是正好填满 4 块，所以实战的时候并没有用到这个 trick。

代码如下，其中调整 gao_block 的参数以对指定 block_id 的密文进行二分：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
from pwn import *
from Crypto.Util.number import *
import string

valid_chars = sorted(list(set(string.printable) - set(string.whitespace)))
valid_chars = [ord(x) for x in valid_chars]

def go_down(n, blocksize=16):
    n_list = list(long_to_bytes(n, blocksize=blocksize))
    for i in range(len(n_list)):
        if (n_list[i] <= 32):
            # jiewei
            n_list[i-1] -= 1
            for j in range(i, len(n_list)):
                n_list[j] = valid_chars[-1]
            break
        elif (n_list[i] >= 127):
            # 
            n_list[i] = valid_chars[-1]
            for k in range(i+1, len(n_list)):
                n_list[k] = valid_chars[-1]
            break
    return bytes(n_list)

class Gao:
    def __init__(self):
        # self.conn = process(['python3', 'another.py'])
        self.conn = remote('02.cr.yp.toc.tf', 31377)
        self.known_boundary = [
            (89407868913636251168773770333092460099, 89407868913636251168773771937085893559),
            (161404117612298851011345476078246390139, 161404117612298851011345476078246485744),
            (109522198106951428429083248646293642604, 109522198106951428429083248646293738208),
            (73653713219403595476250315686409203966, 73653713219403595476250315686421441464)
        ]
    
    def gao_recv(self):
        self.conn.sendline('E')
        self.conn.recvuntil('| encrypt(flag, key, params) = ')
        self.c_list = eval(self.conn.recvline())
    
    def get_encrypt(self, m):
        self.conn.sendline('T')
        self.conn.sendline(m)
        self.conn.recvuntil('| C = ')
        c = eval(self.conn.recvline())[0]
        return c

    def gao_block(self, i):
        c = self.c_list[i]
        # l = bytes_to_long(b'!!!!!!!!!!!!!!!!')
        # r = bytes_to_long(b'~~~~ ~~~~ ~~~~ ~~~~')
        l, r = self.known_boundary[i]
        while (l < r):
            print(f'#{i}: {l = }, {r = }')
            mid = (l + r) >> 1
            mmid = go_down(mid)
            cmid = self.get_encrypt(mmid)
            if (cmid < c):
                l = mid + 1
            else:
                r = mid
        if (l == bytes_to_long(b'!!!!!!!!!!!!!!!!')):
            raise Exception('Error')
        else:
            print(f'AOLIGEI!!! #{i}: {long_to_bytes(l)}')

    def gao(self):
        self.gao_recv()
        self.gao_block(1)

if __name__ == '__main__':
    g = Gao()
    g.gao()

得到 flag 为：

1
CCTF{Boldyreva_5ymMe7rIC_0rD3r_pRe5Erv!n9_3nCryp7i0n!_LStfig9TM}

Bertrand

题目描述

该问题是关于一个对图像进行加密的算法。

值得关注的是，后面有一句

1
assert len(key) == 3

而且稍微关注一下 encrypt 函数，就知道 msg 和 key 都是 str 类型，且一开始用了 ord 转成 ASCII 码，因此还可以大胆猜测 msg 和 key 都是可见字符。

所以就是可以对 key 进行爆破。

然后具体看到 encrypt 加密算法，该算法分为两部分：第一部分将 msg 打乱，第二部分将打乱后的 msg 按照一定顺序填入一个 $n \times n$ 的图像中。

第一部分：打乱 msg

分为如下若干步，迭代 len(key) = 3 次

  1. w: key 的长度
  2. h: 取为 n**2 // w + 1，这样就保证 w * h > n**2
  3. arr: 弄一个 w 行 h 列的的二维数组，将_msg 内容 按列优先 依次填入 arr 中，剩下的元素填 None
  4. _conf: 对 _key 中的 (k_ascii, index) 排序
  5. _marshal: arr[index] 一行一行的，也就是说按照 _key 中 ascii 从小到大的索引，对 arr 的行进行重排
  6. _msg: 将 _marshal 展平为一维数组，并过滤掉 None，最后用 key 中内容进行循环模 256 加的加密。

下面是上述第 3 步的解释：如果我们取 w = 3，h = 4，n = 3，msg = 'wuhudasim'，那么 arr 如下图，其中 / 表示 None：

然后按行打乱得到 _marshal，譬如打乱成

然后展平、过滤掉 None，就得到了 udihamwus，然后与 key 中内容进行循环模 256 加的加密。

第二部分：将密文填入图像

这里定义了一个 sox 函数，用于控制图像上的 $(x, y)$ 坐标演进。通过代码审计，或是简单的调试，可以看到：

  1. 这是一个类似于蛇形的、尝试将 $2^k \times 2^k$ 的坐标铺满的坐标生成方式，其中 $k$ 为满足 $2^k \ge n$ 的最小 $k$
  2. 对于同奇偶的 $n_1, n_2$，如果 $n_1 < n_2$，那么用 $n_1$ 生成的坐标序列是用 $n_2$ 坐标序列的子序列。

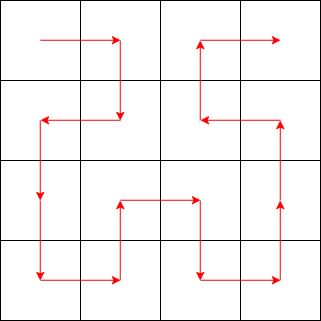
性质一的直观展示如下：

性质二的验证代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
def sox(n, d):
    x, y, t = 0, 0, d
    for s in range(n - 1):
        u = 1 & (t // 2)
        v = (1 & t) ^ u
        x, y = spin(2**s, x, y, u, v)
        x += 2**s * u
        y += 2**s * v
        t = t // 4
    return x, y

def spin(n, x, y, u, v):
    '''
    n: 图像的宽高
    x, y: 横纵坐标
    '''
    if v == 0:
        if u == 1:
            x = n - 1 - x
            y = n - 1 - y
        x, y = y, x
    return x, y

def get_path_sequence(n):
    path_sequence = []
    for d in range(n**2):
        x, y = sox(n, d)
        path_sequence.append((x, y))
    return path_sequence

p3 = get_path_sequence(3)
p5 = get_path_sequence(5)
p7 = get_path_sequence(7)
p233 = get_path_sequence(233)
print(p5[:len(p3)] == p3)
print(p7[:len(p3)] == p3)
print(p233[:len(p7)] == p7)

之后还会根据 sum(key) % 4 的值来对图像进行旋转操作。

分析

所以说，因为之前生成的图像是 $n \times n$ 的，所以就可以通过图像的大小得到 $n$ 的大小。

读进来发现 $n = 256$。

代入第一部分的分析，$w = 3, h = 21846$，这样因为 $256 ^ 2 \equiv 1 \pmod{3}$，所以的话在填 arr 的时候，第 0 行就会填多一个，第 1 行和第 2 行都是填的 None。所以在逆过来，也就是从被压扁的一维数组升到二维数组的时候，要保证把 arr 的行换回去的时候，多出来的东西还是在第 0 行就行了。

另外，对于换位置这种变换，我们可以仅把明文序号代进去，得到加密之后的序号，然后反推即可。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
import cv2
import pickle
import itertools
import functools
from tqdm import tqdm

c = cv2.imread('enc.png', cv2.IMREAD_GRAYSCALE)

n = 256
w = 3
h = n**2 // w + 1

def decrypt(c, key, sox_list):
    orient = sum(key) % 4
    c1 = c.copy()
    for i in range(orient):
        c1 = cv2.rotate(c1, cv2.ROTATE_90_CLOCKWISE)
    
    '''
    Notice np.array coordinate system and PIL.Image counterpart
    '''
    c2 = [c1[y, x] for x, y in sox_list]
    
    '''
    construct index list and apply encryption
    '''
    _msg = list(range(n**2))
    arr = [[_msg[w*x + y] if w*x + y < n**2 else None for x in range(h)] for y in range(w)]
    _conf = sorted([(key[i], i) for i in range(w)])
    _marshal = [arr[_conf[i][1]] for i in range(w)]
    _msg = functools.reduce(lambda a, r: a + _marshal[r], range(w), [])
    _msg = list(filter(lambda x: x is not None, _msg))
    
    '''
    apply decryption
    '''
    for current_iter in range(w):
        c2 = [(x - y) % 256 for x, y in zip(c2, itertools.cycle(key))]
        
        m2 = [None for i in range(n**2)]
        for i in range(n**2):
            m2[_msg[i]] = c2[i]
        c2 = m2
    return bytes(c2)

with open('path_sequence.pickle', 'rb') as f:
    sox_list = pickle.load(f)

for key in tqdm(itertools.product(range(32, 128), repeat=3)):
    msg = decrypt(c, key, sox_list)
    if (b'CCTF{' in msg):
        print('AOLIGEI!!!')
        print(f'key = {key}')
        print(msg)

然后再的时候，会发现运行得非常慢。。。所以在不另谋他法的前提下，需要把上面的代码尝试改成 C++。首先，原生 C++没有图像操作的 API，所以把像素值（包括所有旋转，往回转的）写到文件中，再在 C++中直接操作。同时，由于计算填入图像的坐标比较耗时（需要用到这些坐标，以把二维的图像展成一维的密文）所以也采取先预计算并存文件，再在 C++里面读取的策略。预处理如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
import pickle
import cv2

def spin(n, x, y, u, v):
    if v == 0:
        if u == 1:
            x = n - 1 - x
            y = n - 1 - y
        x, y = y, x
    return x, y

def sox(n, d):
    x, y, t = 0, 0, d
    for s in range(n - 1):
        u = 1 & (t // 2)
        v = (1 & t) ^ u
        x, y = spin(2**s, x, y, u, v)
        x += 2**s * u
        y += 2**s * v
        t = t // 4
    return x, y

n = 256
def get_path_sequence(n):
    path_sequence = []
    for d in range(n**2):
        x, y = sox(n, d)
        path_sequence.append((x, y))
    return path_sequence

s = '\n'.join(f'{x} {y}' for x, y in get_path_sequence(n))
with open('path_sequence.txt', 'w') as f:
    f.write(s)

c = cv2.imread('enc.png', cv2.IMREAD_GRAYSCALE)

assert c.shape[0] == n and c.shape[1] == n
for orient in range(4):
    s = ''
    for i in range(n):
        s += ' '.join(str(c[i, j]) for j in range(n)) + '\n'
    with open(f'pixel_value_{orient}.txt', 'w') as f:
        f.write(s)
    c = cv2.rotate(c, cv2.ROTATE_90_CLOCKWISE)

C++完全从 python 的求解代码改过来。可以采取多线程的技巧。当然，先要在单进程下把程序调通，不然如果连求解的正确性都不能保证的话，那就痛苦了：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
#include <bits/stdc++.h>
using namespace std;

using path_sequence_t = vector<pair<int, int>>;

const int NUM_THREADS = 256;

auto get_path_sequence(int n) {
    ifstream ifs("path_sequence.txt");
    path_sequence_t result;
    for (int i = 0; i < n * n; i++) {
        int x, y;
        ifs >> x >> y;
        result.push_back(make_pair(x, y));
    }
    return result;
}

auto get_rotated_img(int orient, int n, const path_sequence_t& path_sequence) {
    stringstream ss;
    ss << "pixel_value_" << orient << ".txt";
    ifstream ifs(ss.str());
    int v;
    vector<int> result_(n * n);
    vector<int> result(n * n);
    for (int i = 0; i < n * n; i++) {
        ifs >> v;
        result_[i] = v;
    }
    for (int i = 0; i < n * n; i++) {
        int x = path_sequence[i].first, y = path_sequence[i].second;
        // Notice the difference between np.array coordinate system
        // and PIL.Image counterpart
        result[i] = result_[x + y * n];
    }
    return result;
}

void decrypt(int thread_id) {
    const int n = 256;
    const int w = 3;
    const int h = n * n / w + 1;
    const int NONE = -1;
    const char ans[] = "CCTF{";

    auto path_sequence = get_path_sequence(n);
    vector<vector<int>> rotated_img_list(4);
    for (int i = 0; i < 4; i++) {
        rotated_img_list[i] = get_rotated_img(i, n, path_sequence);
    }
    for (int a = thread_id; a < 256; a += NUM_THREADS) {
        // cout << "a = " << a << endl;
        for (int b = 0; b < 256; b++) {
            for (int c = 0; c < 256; c++) {
                vector<int> key{a, b, c};

                // construct index list and apply encryption
                vector<int> _msg(n * n);
                for (int i = 0; i < n * n; i++) {
                    _msg[i] = i;
                }
                vector<vector<int>> arr(w);
                for (int i = 0; i < w; i++) {
                    arr[i].resize(h);
                }
                for (int y = 0; y < w; y++) {
                    for (int x = 0; x < h; x++) {
                        if (w * x + y < n * n) {
                            arr[y][x] = _msg[w * x + y];
                        } else {
                            arr[y][x] = NONE;
                        }
                    }
                }
                vector<pair<int, int>> _conf(w);
                for (int i = 0; i < w; i++) {
                    _conf[i] = make_pair(key[i], i);
                }
                sort(_conf.begin(), _conf.end());
                vector<vector<int>> _marshal(w);
                for (int i = 0; i < w; i++) {
                    _marshal[i] = arr[_conf[i].second];
                }
                int cnt = 0;
                for (int i = 0; i < w; i++) {
                    for (int j = 0; j < h; j++) {
                        if (_marshal[i][j] != NONE) {
                            _msg[cnt] = _marshal[i][j];
                            cnt += 1;
                        }
                    }
                }

                // apply decryption
                int orient = (a + b + c) % 4;
                auto c2 = rotated_img_list[orient];
                for (int current_iter = 0; current_iter < w; current_iter++) {
                    for (int i = 0; i < n * n; i++) {
                        c2[i] = (c2[i] - key[i % w] + 256) % 256;
                    }
                    vector<int> m2(n * n);
                    for (int i = 0; i < n * n; i++) {
                        m2[_msg[i]] = c2[i];
                    }
                    c2 = m2;
                }

                // check
                bool ok = true;
                for (int i = 0; i < 5; i++) {
                    if (c2[i] != ans[i]) {
                        ok = false;
                        break;
                    }
                }
                if (!ok) {
                    continue;
                }
                for (int i = 0; i < n * n; i++) {
                    if (!((c2[i] >= 32) && (c2[i] < 127))) {
                        ok = false;
                        break;
                    }
                }
                if (!ok) {
                    continue;
                }
                cout << "AOLIGEI!!!" << endl;
                cout << "Key = (" << a << ", " << b << ", " << c << ")" << endl;
                cout << "message: ";
                for (int i = 0; i < n * n; i++) {
                    cout << (char)c2[i];
                }
                cout << endl;
            }
        }
    }
}

int main(int argc, char **argv){
    vector<thread> threads(NUM_THREADS);
    for (int i = 0; i < NUM_THREADS; i++) {
        threads[i] = thread(decrypt, i);
    }
    for (int i = 0; i < NUM_THREADS; i++) {
        threads[i].join();
    }
    return 0;
}

编译开启 -O3 优化，链接 pthread：

1
g++ solve.cpp -O3 -lpthread -o solve

在 256 核服务器上也需要跑个几分钟才能跑出结果来。得到 flag 为：

1
CCTF{3nCrypTioN_8Y_c0lUmn4R_7rAnSp05it!On!}

当然还有从算法中着手优化的方法：由于整个算法一路下来是线性的，所以可以跟踪密钥的加密情况。

具体来说，就是可以假设一个 _key 的顺序，就可以得到加密步骤中所有的位置重排。

然后在加每轮密钥的时候，记录加的是哪个密钥；在位置重排的时候，和上面的一样，把 _msg 的索引做重排，然后此时密钥的位置也需要跟着 _msg 的索引进行重排。

然后经过加密流程以后，就可以根据 CCTF{ 的前缀，去建立 $GF(2^8)$ 下的线性方程组，解出密钥。最后根据解出的密钥对密文进行解密。

但是这样做的话，可能有一个坑点：$GF(2^8)$ 下的线性方程组可能会有 2 的系数，这样解出来的密钥是不唯一的。也就是说，sagemath 的 solve_right 方法只能提供一个解，并且对于 $GF(2^8)$，sagemath 是没有实现 right_kernel 的。不过幸亏我们的系数只会走到 2，所以解出来的密钥可以保证模 $2^7$ 的值是没问题的。所以我们就只需要解出一个密钥之后，枚举一下高位就行了。

因为这里我们用 sagemath 做，所以只需要把 sox 函数所生成的路径持久化为 pickle，在代码中再载入就行了。代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
from PIL import Image
import pickle
import itertools
import functools
from tqdm import tqdm

c = Image.open('enc.png').convert('L')
n = 256
w = 3
h = n**2 // w + 1

def decrypt(c, sox_list):
    c1 = c.copy()
    for orient in range(4):
        c1 = c1.rotate(float(-90*orient))
        
        c2 = [c1.getpixel((x, y)) for x, y in sox_list]
        
        '''
        enumerate the possible key rank
        '''
        for k0_rank, k1_rank, k2_rank in itertools.permutations(range(3)):
            '''
            construct index list and apply encryption
            '''
            _msg = list(range(n**2))
            _key = [[] for i in range(n**2)]
            _conf = [k0_rank, k1_rank, k2_rank]
            for current_iter in range(w):
                arr = [[_msg[w*x + y] if w*x + y < n**2 else None for x in range(h)] for y in range(w)]
                keyarr = [[_key[w*x + y] if w*x + y < n**2 else None for x in range(h)] for y in range(w)]
                
                _marshal = [arr[_conf[i]] for i in range(w)]
                _keymarshal = [keyarr[_conf[i]] for i in range(w)]
                _msg = functools.reduce(lambda a, r: a + _marshal[r], range(w), [])
                _msg = list(filter(lambda x: x is not None, _msg))
                _key = functools.reduce(lambda a, r: a + _keymarshal[r], range(w), [])
                _key = list(filter(lambda x: x is not None, _key))
                '''
                add key
                '''
                for i in range(n ** 2):
                    _key[i].append(i % 3)
            
            mindex2cindex = [0 for i in range(n**2)]
            for cindex, mindex in enumerate(_msg):
                mindex2cindex[mindex] = cindex
            dst = b'CCTF{'
            b = [c2[mindex2cindex[i]] - dst[i] for i in range(5)]
            A = [[0 for j in range(3)] for i in range(5)]
            for i in range(5):
                for j in range(3):
                    ki = _key[mindex2cindex[i]][j]
                    A[i][ki] += 1
            
            A = matrix(Zmod(256), A)
            b = vector(Zmod(256), b)

            try:
                x = A.solve_right(b)
            except ValueError:
                # No solution: try another possibility
                continue
            
            k_list_0 = [ZZ(xi) for xi in x.list()]
            for k_list_h in itertools.product(range(2), repeat=3):
                k_list = [(x + 128 * y) % 256 for x, y in zip(k_list_0, k_list_h)]
                '''
                decrypt
                '''
                msg = [0 for i in range(n**2)]
                for i in range(n**2):
                    msg[i] = c2[mindex2cindex[i]]
                    for j in range(3):
                        msg[i] -= ZZ(k_list[_key[mindex2cindex[i]][j]])
                        msg[i] %= 256
                
                if bytes(msg)[:5] == dst:
                    print(bytes(msg)[:50])

with open('path_sequence.pickle', 'rb') as f:
    sox_list = pickle.load(f)

decrypt(c, sox_list)

Insights

题目描述

RSA 中，$p$ 和 $q$ 为 1024 位素数，且高 71 位已知。$N=pq$，$N$ 已知。

解密指数 $d$ 为素数，大概为 $N^{0.2919}$

此外还知道加密指数 $e$ 和密文 $c$，求明文 $m$。

我的解答

解密指数给得非常微妙，正好摸到了 Boneh-Durfee 理论界的顶端。所以一开始会去想莽试一波 Boneh-Durfee。

但是显而易见，这个理论界，就和国足理论上夺取大力神杯一样，太理论了。所以还是需要借助 $p$ 和 $q$ 高位来进行解题。

进一步将高位已知的事实进行形式化：记 $p = p_h + p_l$，$q = q_h + q_l$

那么复习一下，Boneh-Durfee 是利用公钥与私钥之间的关系式：

其中 $s = p + q$

将上式模 $e$ 分析，并记 $A = (N+1) / 2, x = 2k, y=s/2$ 就有：

然后利用 Coppersmith 方法解上式。

类似地，在公钥和私钥的关系式中，将我们已知高位的条件代入进去，可以知道：

所以可以类似地，记 $A = (N+1)/2 - (p_h + q_h)/2, x = 2k, y=(p_l + q_l)/2$ 就有：

就可以用 Coppersmith 方法解，而且问题形式跟上面的一模一样。

然后代码直接根据 RSA-and-LLL-attacks 里面的代码改就行。需要注意里面的默认 $m=4$ 规约出的系数不能保证方程在 $\mathbb{Z}^2$ 上有解，所以需要再调大一点点：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
from __future__ import print_function
import time

############################################
# Config
##########################################

"""
Setting debug to true will display more informations
about the lattice, the bounds, the vectors...
"""
debug = True

"""
Setting strict to true will stop the algorithm (and
return (-1, -1)) if we don't have a correct
upperbound on the determinant. Note that this
doesn't necesseraly mean that no solutions
will be found since the theoretical upperbound is
usualy far away from actual results. That is why
you should probably use `strict = False`
"""
strict = False

"""
This is experimental, but has provided remarkable results
so far. It tries to reduce the lattice as much as it can
while keeping its efficiency. I see no reason not to use
this option, but if things don't work, you should try
disabling it
"""
helpful_only = True
dimension_min = 7 # stop removing if lattice reaches that dimension

############################################
# Functions
##########################################

# display stats on helpful vectors
def helpful_vectors(BB, modulus):
    nothelpful = 0
    for ii in range(BB.dimensions()[0]):
        if BB[ii,ii] >= modulus:
            nothelpful += 1

    print(nothelpful, "/", BB.dimensions()[0], " vectors are not helpful")

# display matrix picture with 0 and X
def matrix_overview(BB, bound):
    for ii in range(BB.dimensions()[0]):
        a = ('%02d ' % ii)
        for jj in range(BB.dimensions()[1]):
            a += '0' if BB[ii,jj] == 0 else 'X'
            if BB.dimensions()[0] < 60:
                a += ' '
        if BB[ii, ii] >= bound:
            a += '~'
        print(a)

# tries to remove unhelpful vectors
# we start at current = n-1 (last vector)
def remove_unhelpful(BB, monomials, bound, current):
    # end of our recursive function
    if current == -1 or BB.dimensions()[0] <= dimension_min:
        return BB

    # we start by checking from the end
    for ii in range(current, -1, -1):
        # if it is unhelpful:
        if BB[ii, ii] >= bound:
            affected_vectors = 0
            affected_vector_index = 0
            # let's check if it affects other vectors
            for jj in range(ii + 1, BB.dimensions()[0]):
                # if another vector is affected:
                # we increase the count
                if BB[jj, ii] != 0:
                    affected_vectors += 1
                    affected_vector_index = jj

            # level: 0
            # if no other vectors end up affected
            # we remove it
            if affected_vectors == 0:
                print("* removing unhelpful vector", ii)
                BB = BB.delete_columns([ii])
                BB = BB.delete_rows([ii])
                monomials.pop(ii)
                BB = remove_unhelpful(BB, monomials, bound, ii-1)
                return BB

            # level: 1
            # if just one was affected we check
            # if it is affecting someone else
            elif affected_vectors == 1:
                affected_deeper = True
                for kk in range(affected_vector_index + 1, BB.dimensions()[0]):
                    # if it is affecting even one vector
                    # we give up on this one
                    if BB[kk, affected_vector_index] != 0:
                        affected_deeper = False
                # remove both it if no other vector was affected and
                # this helpful vector is not helpful enough
                # compared to our unhelpful one
                if affected_deeper and abs(bound - BB[affected_vector_index, affected_vector_index]) < abs(bound - BB[ii, ii]):
                    print("* removing unhelpful vectors", ii, "and", affected_vector_index)
                    BB = BB.delete_columns([affected_vector_index, ii])
                    BB = BB.delete_rows([affected_vector_index, ii])
                    monomials.pop(affected_vector_index)
                    monomials.pop(ii)
                    BB = remove_unhelpful(BB, monomials, bound, ii-1)
                    return BB
    # nothing happened
    return BB

""" 
Returns:
* 0,0   if it fails
* -1,-1 if `strict=true`, and determinant doesn't bound
* x0,y0 the solutions of `pol`
"""
def boneh_durfee(pol, modulus, mm, tt, XX, YY):
    """
    Boneh and Durfee revisited by Herrmann and May
    
    finds a solution if:
    * d < N^delta
    * |x| < e^delta
    * |y| < e^0.5
    whenever delta < 1 - sqrt(2)/2 ~ 0.292
    """

    # substitution (Herrman and May)
    PR.<u, x, y> = PolynomialRing(ZZ)
    Q = PR.quotient(x*y + 1 - u) # u = xy + 1
    polZ = Q(pol).lift()

    UU = XX*YY + 1

    # x-shifts
    gg = []
    for kk in range(mm + 1):
        for ii in range(mm - kk + 1):
            xshift = x^ii * modulus^(mm - kk) * polZ(u, x, y)^kk
            gg.append(xshift)
    gg.sort()

    # x-shifts list of monomials
    monomials = []
    for polynomial in gg:
        for monomial in polynomial.monomials():
            if monomial not in monomials:
                monomials.append(monomial)
    monomials.sort()
    
    # y-shifts (selected by Herrman and May)
    for jj in range(1, tt + 1):
        for kk in range(floor(mm/tt) * jj, mm + 1):
            yshift = y^jj * polZ(u, x, y)^kk * modulus^(mm - kk)
            yshift = Q(yshift).lift()
            gg.append(yshift) # substitution
    
    # y-shifts list of monomials
    for jj in range(1, tt + 1):
        for kk in range(floor(mm/tt) * jj, mm + 1):
            monomials.append(u^kk * y^jj)

    # construct lattice B
    nn = len(monomials)
    BB = Matrix(ZZ, nn)
    for ii in range(nn):
        BB[ii, 0] = gg[ii](0, 0, 0)
        for jj in range(1, ii + 1):
            if monomials[jj] in gg[ii].monomials():
                BB[ii, jj] = gg[ii].monomial_coefficient(monomials[jj]) * monomials[jj](UU,XX,YY)

    # Prototype to reduce the lattice
    if helpful_only:
        # automatically remove
        BB = remove_unhelpful(BB, monomials, modulus^mm, nn-1)
        # reset dimension
        nn = BB.dimensions()[0]
        if nn == 0:
            print("failure")
            return 0,0

    # check if vectors are helpful
    if debug:
        helpful_vectors(BB, modulus^mm)
    
    # check if determinant is correctly bounded
    det = BB.det()
    bound = modulus^(mm*nn)
    if det >= bound:
        print("We do not have det < bound. Solutions might not be found.")
        print("Try with highers m and t.")
        if debug:
            diff = (log(det) - log(bound)) / log(2)
            print("size det(L) - size e^(m*n) = ", floor(diff))
        if strict:
            return -1, -1
    else:
        print("det(L) < e^(m*n) (good! If a solution exists < N^delta, it will be found)")

    # display the lattice basis
    if debug:
        matrix_overview(BB, modulus^mm)

    # LLL
    if debug:
        print("optimizing basis of the lattice via LLL, this can take a long time")

    BB = BB.LLL()

    if debug:
        print("LLL is done!")

    # transform vector i & j -> polynomials 1 & 2
    if debug:
        print("looking for independent vectors in the lattice")
    found_polynomials = False
    
    for pol1_idx in range(nn - 1):
        for pol2_idx in range(pol1_idx + 1, nn):
            # for i and j, create the two polynomials
            PR.<w,z> = PolynomialRing(ZZ)
            pol1 = pol2 = 0
            for jj in range(nn):
                pol1 += monomials[jj](w*z+1,w,z) * BB[pol1_idx, jj] / monomials[jj](UU,XX,YY)
                pol2 += monomials[jj](w*z+1,w,z) * BB[pol2_idx, jj] / monomials[jj](UU,XX,YY)

            # resultant
            PR.<q> = PolynomialRing(ZZ)
            rr = pol1.resultant(pol2)

            # are these good polynomials?
            if rr.is_zero() or rr.monomials() == [1]:
                continue
            else:
                print("found them, using vectors", pol1_idx, "and", pol2_idx)
                found_polynomials = True
                break
        if found_polynomials:
            break

    if not found_polynomials:
        print("no independant vectors could be found. This should very rarely happen...")
        return 0, 0
    
    rr = rr(q, q)

    # solutions
    soly = rr.roots()

    if len(soly) == 0:
        print("Your prediction (delta) is too small")
        return 0, 0

    soly = soly[0][0]
    ss = pol1(q, soly)
    solx = ss.roots()[0][0]

    #

    return solx, soly

def example():
    ############################################
    # How To Use This Script
    ##########################################

    #

    # The problem to solve (edit the following values)
    #


    # the modulus
    N = 12765231982257032754070342601068819788671760506321816381988340379929052646067454855779362773785313297204165444163623633335057895252608396010414744222572161530653104640020689896882490979790275711854268113058363186249545193245142912930804650114934761299016468156185416083682476142929968501395899099376750415294540156026131156551291971922076435528869024742993840057342092865203064721826362149723366381892539617642364692012936270150691803063945919154346756726869466855557344213050973081755499746750276623648407677639812809665472258655462846021403503851719008687214848550916999977775070011121527941755954255781343103086789
    # the public exponent
    e = 459650454686946706615371845737527916539205656667844780634386049268800615782964920944229084502752167395446158290854047696006034750210758341744841762479191173017773034647739346927390580848998121830029134542880713409306092967282675122699586503684943407535067216738556403169403622104762516293879994387324370835718056251706150557820106296417750402984941838652433642298378976899556042987560946508887315484380807248331504458640857234708123277403252632993828101306072382329879857946191508782246793011691530554606521701055094223574951862129713872918021549814674387049788995785872980320871421550616327471735316980754238323013
    L = 0b10100000111001001100001011000110111010001101001011000110110000101101100
    
    sh = L << (1024 - 71)

    # the hypothesis on the private exponent (the theoretical maximum is 0.292)
    delta = .292 # this means that d < N^delta

    #

    # Lattice (tweak those values)
    #


    # you should tweak this (after a first run), (e.g. increment it until a solution is found)
    m = 6 # size of the lattice (bigger the better/slower)

    # you need to be a lattice master to tweak these
    t = int((1-2*delta) * m)  # optimization from Herrmann and May
    X = floor(N^delta)  # this _might_ be too much
    Y = floor(2^953)    # correct if p, q are ~ same size

    #

    # Don't touch anything below
    #


    # Problem put in equation
    P.<x,y> = PolynomialRing(ZZ)
    A = int((N+1)/2 - sh)
    pol = 1 + x * (A + y)
    '''
    e d = 1 + k (p-1) (q-1)

    e d = 1 + k (N+1) + k s

    e d = 1 + 2k ((N+1)/2 + s/2)

    e d = 1 + 2k ((N+1)/2 + sh/2 + sl/2)
    '''

    #

    # Find the solutions!
    #


    # Checking bounds
    if debug:
        print("=== checking values ===")
        print("* delta:", delta)
        print("* delta < 0.292", delta < 0.292)
        print("* size of e:", int(log(e)/log(2)))
        print("* size of N:", int(log(N)/log(2)))
        print("* m:", m, ", t:", t)

    # boneh_durfee
    if debug:
        print("=== running algorithm ===")
        start_time = time.time()

    solx, soly = boneh_durfee(pol, e, m, t, X, Y)

    # found a solution?
    if solx > 0:
        print("=== solution found ===")
        if False:
            print("x:", solx)
            print("y:", soly)

        d = int(pol(solx, soly) / e)
        print("private key found:", d)
    else:
        print("=== no solution was found ===")

    if debug:
        print(("=== %s seconds ===" % (time.time() - start_time)))

if __name__ == "__main__":
    example()

解得私钥 $d$ 之后解密：

1
2
3
4
5
6
7
8
9
10
from Crypto.Util.number import *

n = 12765231982257032754070342601068819788671760506321816381988340379929052646067454855779362773785313297204165444163623633335057895252608396010414744222572161530653104640020689896882490979790275711854268113058363186249545193245142912930804650114934761299016468156185416083682476142929968501395899099376750415294540156026131156551291971922076435528869024742993840057342092865203064721826362149723366381892539617642364692012936270150691803063945919154346756726869466855557344213050973081755499746750276623648407677639812809665472258655462846021403503851719008687214848550916999977775070011121527941755954255781343103086789
e = 459650454686946706615371845737527916539205656667844780634386049268800615782964920944229084502752167395446158290854047696006034750210758341744841762479191173017773034647739346927390580848998121830029134542880713409306092967282675122699586503684943407535067216738556403169403622104762516293879994387324370835718056251706150557820106296417750402984941838652433642298378976899556042987560946508887315484380807248331504458640857234708123277403252632993828101306072382329879857946191508782246793011691530554606521701055094223574951862129713872918021549814674387049788995785872980320871421550616327471735316980754238323013
c = 10992248752412909788626396175372747713079469256270100576886987393986576680666320383209810005318254336440105142571546847427454822405793626080251363454531982746373841267986148332456716023293306870382809568309620264499225135226626560298741596462262513921032733814032790312163314776421380481083058518893602887082464123177575742160690315666730642727773288362853901330620841098230284739614618790097180848133698381487679399364400048499041582830157094876815030301231505774900176910650887780842536610942820066913075027528705150102760422836458745949063992228680293226303245265232017738712226154128654682937687199768621565945171

d = 693984516363754919249700902493753051718166208912377865278483876234349619419200560616162942304659132290614866566556420934365717915837808485622613368180482591406570741380374249603517

m = pow(c, d, n)
print(long_to_bytes(m))

得到明文：

1
CCTF{RSA_N3w_rEc0rd5_4Nd_nEw_!nSi9h75!}