李宏毅强化学习个人笔记 - Actor-Critic

• 回到概览

A3C: Asynchronous Advantage Actor-Critic

A2C: Advantage Actor-Critic

复习 policy gradient

之前用 policy gradient 去学习 actor 的时候，都是看奖励函数的输出，来决定 actor 要怎么更新，才能得到最大的奖励。

但是因为互动的过程中有非常大的随机性，所以直接根据互动的过程学可能没有办法学得很好。

$$\nabla \bar{R}_{\theta} \approx \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_n} \left( \sum_{t'=t}^{T_n} \gamma^{t'-t} r_{t'}^n - b \right) \nabla \log p_{\theta} (a_t^n | s_t^n)$$

从 $t$ 到 $T_n$ 的奖励加起来，乘上一个随时间减少的衰减因子，再减去一个 bias（baseline）。

可以记 $G_{t}^n = \sum_{t’=t}^{T_n} \gamma^{t’-t} r_{t’}^n$，$G_{t}^n$ 可看成一个随机变量。

在状态 $s$ 后采取动作 $a$，之后的游戏过程是有随机性的，差别可能会很大。

理论上的假设（大数定律）：在足够采样次数之后，可以近似到 $G$ 的期望值。但是因为标准差很大，所以需要采样过多的次数，难以达到。

所以说，能否用一个网络来估测 $G$ 的期望值？如果这样可行的话，可以用网络产生的期望值来代替采样得到的值，这样训练就会更加稳定。

复习 Q-learning

有两种函数（critic）

• 状态值函数 $V^{\pi}(s)$：拿 actor $\pi$ 跟环境做互动，看到状态 $s$ 之后，累积奖励的期望值是多少
• 状态-动作值函数 $Q^{\pi}(s, a)$：拿 actor $\pi$ 跟环境做互动，看到状态 $s$ 时强制选择动作 $a$ 之后，累积奖励的期望值是多少

Actor-Critic

Actor-Critic 的精神：

• actor 不要去看奖励，因为奖励由于环境的影响变化很大；
• actor 不跟环境学，而是跟 critic 学

在 policy gradient 中，$G$ 的期望值究竟是什么？下面这个式子符合 Q 的定义：

$$\mathbb{E}[G_{t}^{n}]=Q^{\pi_\theta}(s_t^n, a_t^n)$$

先估计 Q 函数，然后再把 Q 函数代在算 $\nabla \bar{R}_{\theta}$ 的式子里面，就结束了。

Baseline：直接用 $V^{\pi_\theta}(s_t^{n})$ 就好，也就是说，不考虑在状态 $s_t^n$ 的时候一定要执行哪个动作。$V$ 会是 $Q$ 的期望值。这样，括号里面的东西就会有正有负。也就是：

$$\nabla \bar{R}_{\theta} \approx \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_n} \left( Q^{\pi_\theta}(s_t^n, a_t^n) - V^{\pi_\theta}(s_t^{n}) \right) \nabla \log p_{\theta} (a_t^n | s_t^n)$$

Advantage Actor-Critic

所以 Actor-Critic 的重点就在估计：

$$Q^{\pi}(s_t^n, a_t^n) - V^{\pi}(s_t^{n})$$

而事实上，可以仅用一个网络就把 $Q$ 和 $V$ 都估计了，这样会比用两个网络（估不准的）风险更低。

$$Q^{\pi}(s_t^n, a_t^n) = \mathbb{E}(r_t^n + V^{\pi}(s_{t+1}^n))$$

这里 $r_t$ 是一个随机变量：在状态 $s_t$ 采取动作 $a_t$ 所得到的奖励可能是随机的；以及，跳到的下一个状态 $s_{t+1}$ 也是具有随机性的，为了考虑到随机性，需要加上期望算子。

现在我们把期望值给去掉，当作 Q 函数等于 $r$ 加上 V：

$$Q^{\pi}(s_t^n, a_t^n) = r_t^n + V^{\pi}(s_{t+1}^n)$$

所以待估计的东西就变成了：

$$r_t^n + V^{\pi}(s_{t+1}^n) - V^{\pi}(s_t^{n})$$

这样就只需要估计 V 值了，但是引入了 $r_t$ 这个随机变量。然而，这只有一步的奖励，标准差较小，所以影响不大（较之前 policy gradient 要算累积奖励而言）。

（另一说原始 A3C 的方法直接大力出奇迹，把所有能试的方法都试了个遍，最后发现这样弄就是最好的）

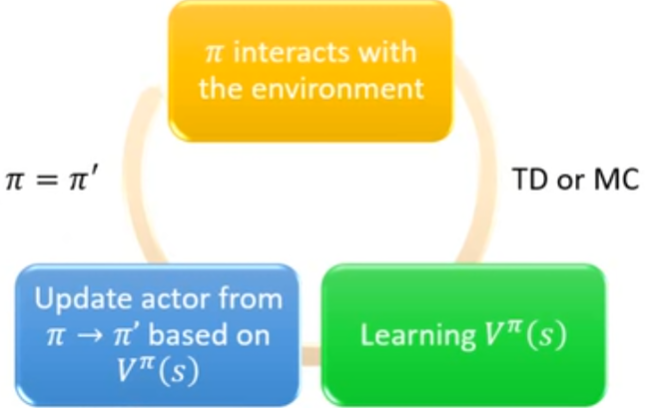
所以，先估计 V 值，然后根据式子：

$$\nabla \bar{R}_{\theta} \approx \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_n} \left( r_t^n + V^{\pi}(s_{t+1}^n) - V^{\pi}(s_t^{n}) \right) \nabla \log p_{\theta} (a_t^n | s_t^n)$$

来更新 policy（更新 actor）

实操的注意事项

• actor $\pi(s)$ 和 critic $V^{\pi}(s)$ 的参数可以共享

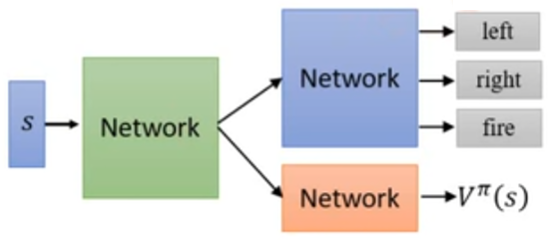
这样做的目的是：

1. actor 和 critic 的输入均为状态 $s$
2. 如果状态输入较复杂（譬如玩视频游戏，输入状态 $s$ 为图像，要先用 CNN 之类的特征抽取器抽取成高级特征），“抽取状态的特征”这件事情可以一次做完

• 需要 exploration 的机制：对 actor $\pi$ 的输出做一个限制：输出分布的熵不应太小，这样在测试的时候才会尝试不同的动作，得到比较好的结果。

Asynchronous Advantage Actor-Critic (A3C)

参考《火影忍者》里面卡卡西叫鸣人开多重影分身来修炼忍术，这样获取到的经验值翻倍

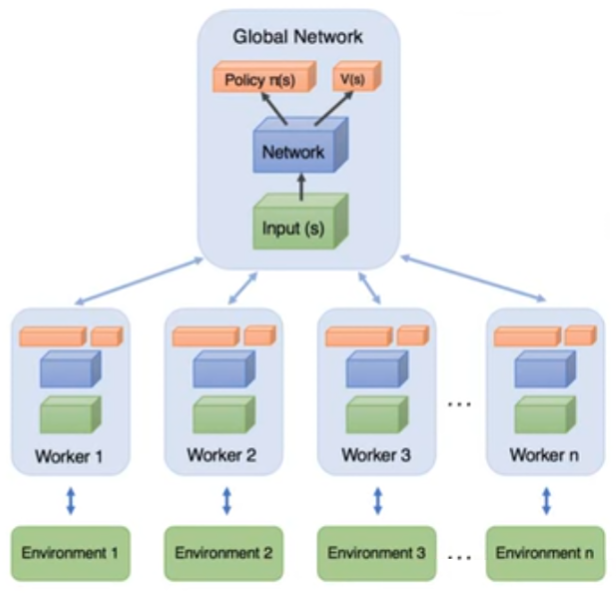
开多个 worker（影分身），来跟环境互动。影分身会把所有的经验集合在一起。

需要多个 CPU。

一开始有一个 Global Network，参数为 $\theta^1$

worker 的工作流程：

1. 拷贝全局参数
2. 采样到一些数据
3. 计算梯度
4. 更新全局模型

$$\theta^2 \leftarrow \theta^1 + \eta \nabla \theta$$

其他 worker 也会对网络参数进行更新

Pathwise Derivative Policy Gradient

可以看成是一种用 Q-learning 解连续动作空间的方法，也可以看成是一种特别的 Actor-Critic 方法

《棋魂》中，佐为在进藤光比较菜的时候面对一个局面建议下小飞；而在进藤光棋艺长进之后，面对相同的局面，则是不建议下小飞，而建议下大飞。

也就是说，actor 在训练中不同的阶段时，critic 会给出不同的打分。

Pathwise Derivative Policy Gradient: Critic 直接告诉 actor 什么样的动作是好的。

回想 Q-learning：动作 $a$ 时连续向量时，$a = \arg \max_{a} Q(s, a)$

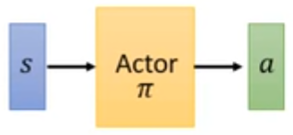
• Q-learning 的改进：在 Pathwise Derivative Policy Gradient 时，actor 直接用于解这个最优化问题（被当作是求解这个最优化问题的求解器）：输入一个状态 $s$，输出最优动作 $a$

• 对比 GAN：Discriminator 本身不知道怎么生成样本才好，就用 generator 来生成。

实际算法

假设学了一个 Q 函数 $Q^{\pi}(s, a)$，接下来要学习一个 actor，用来解

$$\pi'(s) = \arg \max_{a} Q^{\pi}(s, a)$$

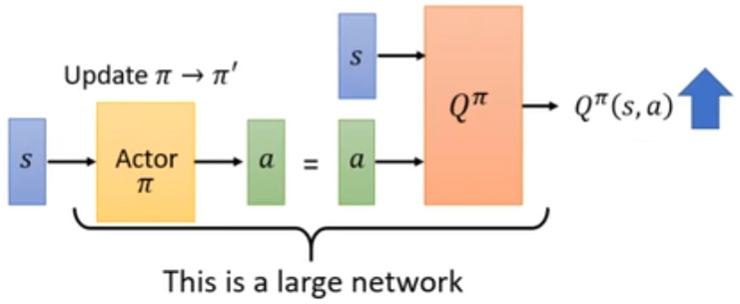
实际上在训练的时候，就把 Q 和 actor 接起来，变成一个更大的网络。

把 Q 的参数冻结起来，只调 actor 的参数 $\pi \to \pi’$，来让 actor 对于状态 $s$，输出最优的动作 $a$。

这下就非常像 GAN 了：actor 就像 generator，Q 就像 discriminator

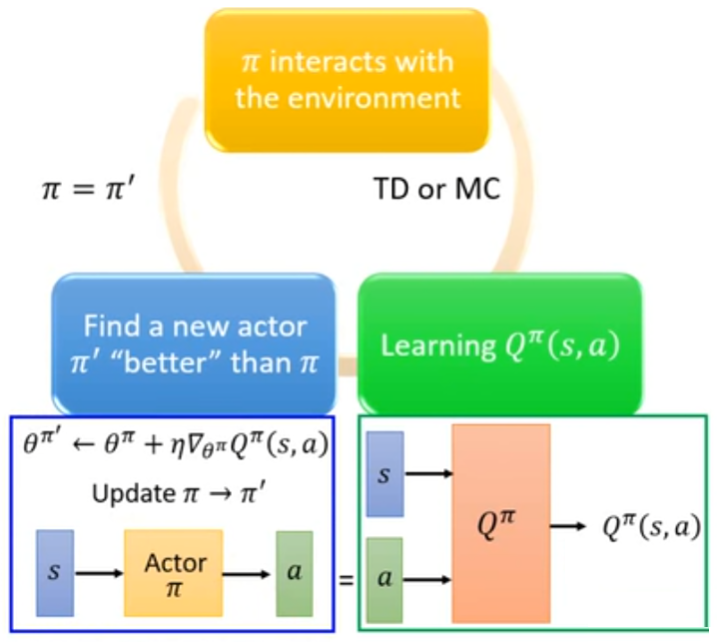
Q-learning 里面所用到的技巧，如 replay buffer、exploration 等，在这里也可以用得上。

对比 Q-learning 的训练流程，我们也可以写出 Pathwise Derivative Policy Gradient 的训练流程如下：

1. 初始化 Q 函数 $Q$ 以及 actor $\pi$，设目标 Q 函数 $\hat{Q} = Q$ 以及 actor $\hat{\pi} = \pi$。
2. 在每个 episode：拿 agent 跟环境去互动。对于每一步 $t$：
   1. 给定状态 $s_t$，基于现在的 $\pi$，采用探索机制（epsilon greedy，Boltzmann exploration），采取动作 $a_t$
   2. 得到奖励 $r_t$，得到新的状态 $s_{t+1}$。至此得到了一个数据 $(s_t, a_t, r_t, s_{t+1})$
   3. 将这个数据 $(s_t, a_t, r_t, s_{t+1})$ 丢到 buffer 里面（如果 buffer 满了，就把最旧的一个数据丢掉）
   4. 从 buffer 中采样 一批 数据 $(s_i, a_i, r_i, s_{i+1})$（刚才放进去的数据可能没被采样到）
   5. 回归目标 $y = r_i + \hat{Q}(s_{i+1}, \hat{\pi}(s_{i+1}))$（回归目标要用目标网络 $\hat{Q}$ 来算）
   6. 更新 $Q$ 的参数，以使 $Q(s_i, a_i)$ 的值尽可能靠近 $y$（回归问题）
   7. 更新 $\pi$ 的参数，以最大化 $Q(s_i, \pi(s_i))$
   8. 每 $C$ 次重设 $\hat{Q}$ 的参数 $\hat{Q} = Q$
   9. 每 $C$ 次重设 $\hat{\pi}$ 的参数 $\hat{\pi} = \pi$

所以说，就是：

1. 多了个 actor $\pi$
2. 在回归目标 $y$ 的计算的时候，也是把 $\hat{\pi}(s_{i+1})$ 丢到了 max 计算式里面
3. $\pi$ 的参数更新：最大化 $Q(s_i, \pi(s_i))$

GAN 和 actor-critic 都是以难训练而闻名的，更多训练技巧可以参考：

Connecting Generative Adversarial Networks and Actor-Critic Methods