跟 policy gradient 比较起来，Q-learning 比较稳定（policy gradient 玩不起来什么游戏）

Q-learning 一个比较好训练的理由是：只要你找得到一个比较好的 Q 函数，那么你就有一个比较好的策略；也就是说如果你能恰当估计 Q 函数（其实比较容易，就是一个回归问题，只需要看到 loss 有无下降就能看出模型学得好不好），你就能更新你的策略。

Q-learning 最大的一个问题就是：比较难处理连续动作的情形。

假设现在动作 $a$ 是一个 连续向量，首先就不能通过枚举所有的 $a$ 去求 argmax。

解法一

对于连续的动作 $a$，对其抽样：抽样出一个动作的集合 $\{a_1, a_2, \ldots, a_N\}$，看看哪个动作能得到最大的 Q 值。

在实际的操作上，可以抽样完后都丢到 Q 函数里面算。因为实际都在用 GPU 进行张量计算，所以也没有到很慢。

但是，采样毕竟不是个精确的方法。可能存在没抽到的更优的动作。

解法二

用梯度上升法来解这个最优化问题。

最小化就用梯度下降，最大化就相应地用梯度上升。

这样做就会碰到陷入局部最优的问题当中，而且因为梯度上升需要逐步迭代，所以计算成本相应地也增大了，训练就更花时间。

解法三

特别设计 Q 网络的架构，使得解 argmax 最优化问题更加简单。

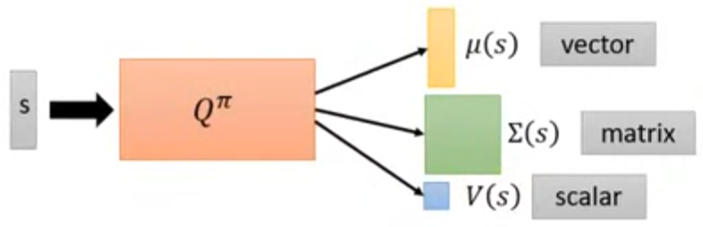
譬如上图的例子：将 $Q^{\pi}$ 关于 $s$ 的部分拆成 $\mu(s)$、$\Sigma(s)$ 和 $V(s)$。

然后将 $Q(s, a)$ 写成 $V(s)$ 加上一个二次型：

这里 $a$ 是一个连续向量：譬如今天的任务是要操控一个机器人，那么 $a$ 的每个维度可能对应机器人每个关节的角度。$\mu(s)$ 的维数跟 $a$ 的维数

假设 $\Sigma(s)$ 是正定的，因为 $Q(s, a)$ 前面那一项一定是非正的，所以现在 $a = \arg \max_{a} Q(s, a)$ 的解就变成了：

  • 将 $a$ 看成一个 n 维高斯分布，对其建模，$\mu(s)$ 和 $\Sigma(s)$ 对应它们的均值和标准差，所以 $\Sigma(s)$ 是正定的
  • 其实 $Q^{\pi}$ 里面不是直接输出 $\Sigma(s)$，而是输出一个矩阵，然后跟自身的转置相乘，得到一个正定矩阵 $\Sigma(s)$

所以这样设计完 Q 网络的架构后，直接代入 $a = \mu(s)$ 就行了。

解法四

不要用 Q-learning

  • Policy-based：PPO
  • Value-based：Q-learning
  • 两者结合：Actor-Critic

尝试用 Actor-Critic 解决连续动作的情形