李宏毅强化学习个人笔记 - Q-learning 在训练时的一些技巧
Double DQN
Double DQN 提出的动机:在实际的 Q-learning 中,Q 值是经常被高估的。
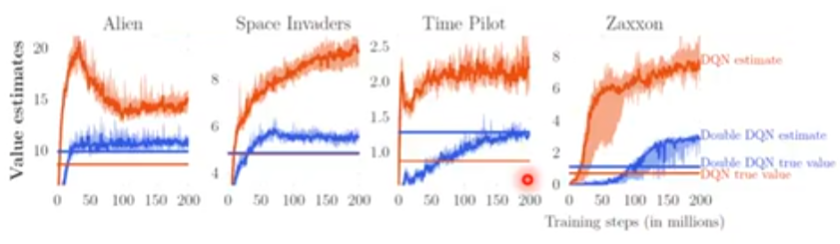
总体来说,DQN 的 Q 值随着训练的进行逐步上升。Q 函数依赖于策略,在学习的过程中,策略会变得越来越强,Q 值就会越来越大。
实际值:训练结束后,再和环境互动,得到的真实奖励。(互动多次取期望)
Double DQN 能让估测值跟实际值更接近,且实际值(真正的累计期望)比原来的 DQN 要更大(模型更强)。
为什么 DQN 中的 Q 值老是被高估? 注意到学习时回归问题的形式:
目标值很容易一不小心就被设太高:在算目标值的时候,看哪一个 $a$ 能得到最大的 $Q$ 值,就把它加上去。假设现在有某个动作 $a$,它得到的 $Q$ 值是被高估的。那么,在回归的时候,总是会选这个被高估的值来作为目标。如下图,本来大家的真实 Q 值都是差不多的,绿色部分表示被高估,那么总会采取被高估的动作对应的 Q 值作为回归目标。
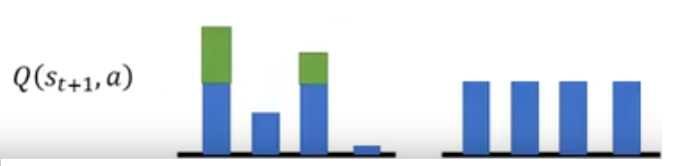
这样,回归训练出的的结果也会跟着变大。
Double DQN 的设计 选动作的 Q 函数($Q$)和算 Q 值的 Q 函数($Q’$)是不同的!
- $Q$:将所有状态 $a$ 都代进 $Q$ 网络中,看看哪一个 Q 值最大
- $Q’$:实际计算 Q 值
为什么这就能避免 Q 值被高估的问题:假设 $Q$ 高估了动作 $a$,只要 $Q’$ 没有高估动作 $a$ 的 Q 值,那么算出来的 Q 值就还是正常的;反过来,假设 $Q’$ 高估了某个动作 $a$ 的 Q 值,只要 $Q$ 不要选到这个动作,就不会算出那个不正常的 Q 值。(参考三权分立,$Q$ 负责提案,$Q’$ 负责执行)
所以实际上,我们会拿待更新参数的网络 $Q$ 来选动作,拿更新缓慢的网络 $Q’$ 来算 Q 值。
(这个改动没有增加运算量,基本上改一行代码的事情,易于实现)
Dueling DQN
Dueling DQN 改了 Q 网络的架构
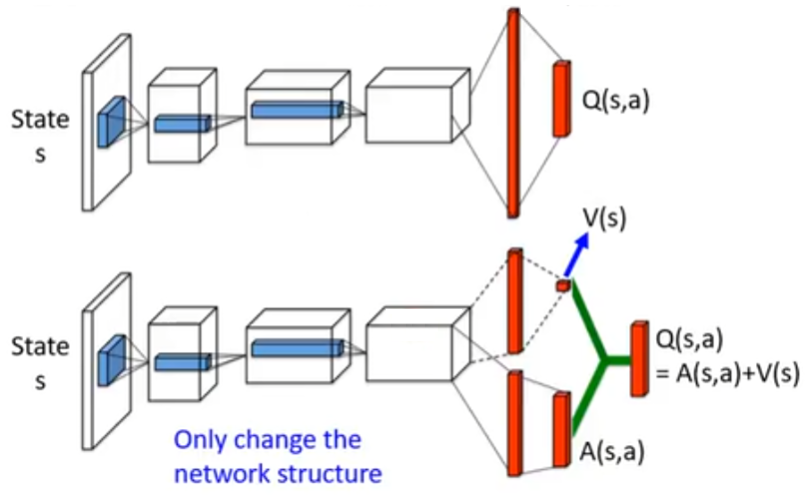
把 $Q(s, a)$ 拆成 $V(s)$ 和 $A(s, a)$。网络结构分成两路运算:
- 对于状态 $s$ 的累积奖励估计 $V(s)$,这是一个标量
- 对于状态 $s$ 和动作 $a$ 的累积奖励估计 $A(s, a)$,也就是对每一个动作 $a$,都有一个 $A(s, a)$ 的值
这样拆分的好处:在训练的时候,不能直接去改 Q 值,只能直接去改 V 值和 A 值。对于某一个状态,它的大部分动作的 Q 都要增加的情况,网络会更可能去调大 V 的值。这样,其他那些(可能就没什么机会采样到的)动作的 Q 也会跟着增加了,这样更新就会更高效。
但是这样拆分可能会有一个退化情况:$V(s) = 0, A(s, a) = Q(s, a)$,这样就相当于啥都没干。为了避免这个情况,会对 $A(s, a)$ 加一些限制,使得模型对 $A(s, a)$ 的改动变得更麻烦。
譬如,让 $\sum_{a}{A(s, a)} = 0$。这样 $V(s)就变成了$ Q(s, a)$关于动作$ a $的平均值。实操的时候,就让$ A(s, a)$在和$ V(s)$相加前进行一个归一化(减去均值)。
Prioritized Replay
在从 buffer 中采样的时候,原来我们是对于所有的数据进行均匀采样。
Prioritized Replay 的核心思想就是:在之前训练中具有更大 TD(回归)误差的数据在之后的训练中有更高的被采样到的概率。
参数更新的过程也被修改了。
Multi-step
结合 MC 和 TD 的采样方法。
在 TD 里面,只往后采样一步,得到数据 $(s_t, a_t, r_t, s_{t+1})$
但是,可以往后采样 $N+1$ 步,得到数据 $(s_t, a_t, r_t, \ldots, s_{t+N}, a_{t+N}, r_{t+N}, s_{t+N+1})$
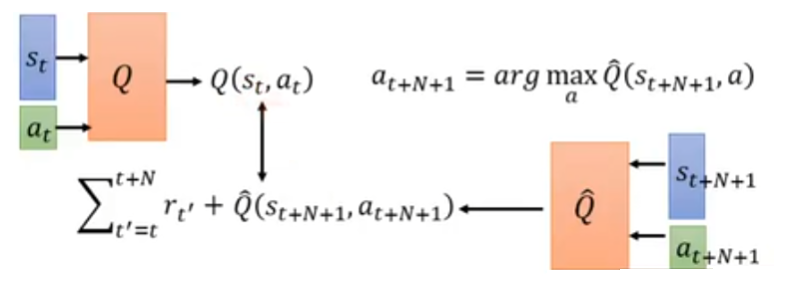
于是,训练过程和回归问题就变成上图所示了。
采样多步,才进行估测,估测部分造成的影响就会比较轻微;但是同样地,把若干步的奖励加起来,方差会较大。调 N 值使得方差增大和 Q 被高估的影响达到一个平衡。
Noisy Net
在网络参数上引入噪声
- 在动作上引入噪声:epsilon greedy
- 在网络参数上引入噪声:每次 在一个 episode 最开始的时候,将 Q 函数的参数加上高斯噪声,得到 $\tilde{Q}$。此时,动作 $a = \arg \max_{a} \tilde{Q}(s, a)$。在同一个 episode,用同一个 $\tilde{Q}$ 和环境互动
- 在动作上引入噪声:在同一个状态中,agent 可能采取不同的动作。但是没有策略真的会在现实中这样做(给同样的状态,应该有同样的回应)
- 在网络参数上引入噪声:在同一个 episode 里面,网络参数都是固定的。这样,看到相似的状态,agent 会采取相同的动作。这被称为 state-dependent exploration(有系统的尝试)
Distributional Q-function
实操时比较少人用
- $Q^{\pi}(s, a)$:状态-动作值函数
- 在使用 actor $\pi$ 的时候,看到状态 $s$ 强制采取动作 $a$ 的累积奖励 期望值
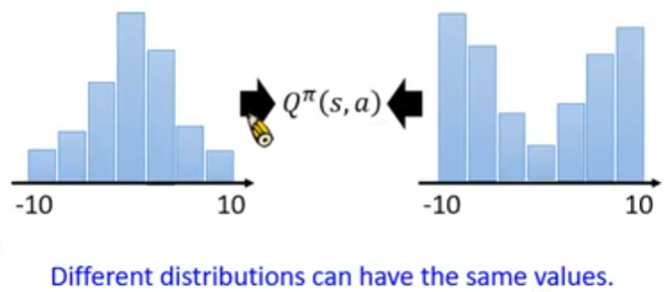
- 也就是说,实际上 $Q^{\pi}(s, a)$ 是一个分布,而不同的分布可能会得出相同的期望值。也就是说,相同的期望值可能对应不同的分布,只关注期望值可能丢失了分布信息
- 所以说,尝试对 $Q^{\pi}(s, a)$ 这个分布建模
- 但是,很可能 $Q^{\pi}(s, a)$ 是个连续值,无法枚举 → 将 $Q^{\pi}(s, a)$ 的值域进行分桶
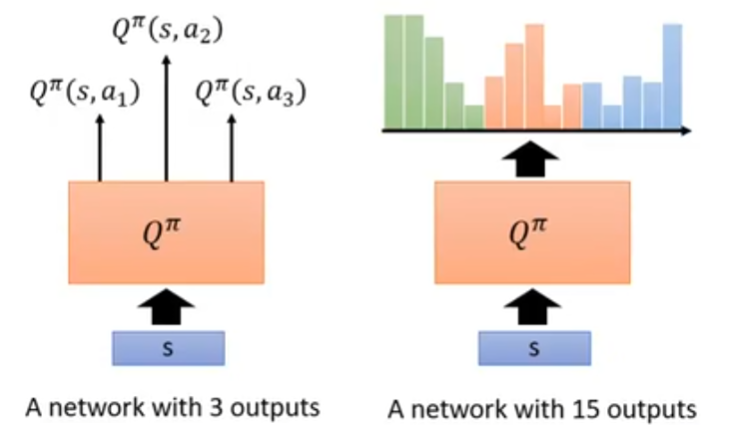
- 譬如下图,看到状态 $s$ 后,能够采取 3 个动作;对每个动作,各自把 Q 值分成 5 个桶,求出 Q 值在这 5 个桶内的分布。
- 选动作:还是选均值最大的动作,但是可以(譬如标准差过大,也就意味着执行该动作的风险很大;为了规避风险,可以尝试选标准差较小的动作去执行)
- 具体怎么训练这个网络需要自行了解
Rainbow
把之前的方法都用起来,大力出奇迹
- DQN(baseline)
- A3C(another baseline)(A3C 中本身就有 multi-step 的策略)
- DDQN
- Prioritized DDQN
- Dueling DDQN
- Distributional DQN
- Noisy DQN
- 把前面都弄起来,就是 Rainbow
然后还有消融实验,结果就是说 distributional Q-function 就是用来防止高估奖励的,所以说把 double DQN 摘了的话,还有 distributional Q-function 来防止高估,所以不会差太多;但是相反,distributional Q-function 可能导致低估奖励,因为分桶的过程可能会裁剪掉极端值。