李宏毅强化学习个人笔记 - Q-learning 简介

• 回到概览

Q-learning 是基于值的方法。我们并不学习策略（Actor），而是学习 Critic。Critic 不直接采取行为，而是评价现在的行为有多好。

假设现在有一个 actor $\pi$，critic 的工作就是评价这个 actor $\pi$ 做得有多好。

譬如这个 critic 可以做成是跟状态有关的函数：$V^{\pi}(s)$。它的含义为使用 actor $\pi$ 时，到了状态 $s$ 之后，可获得的 期望累积奖励。

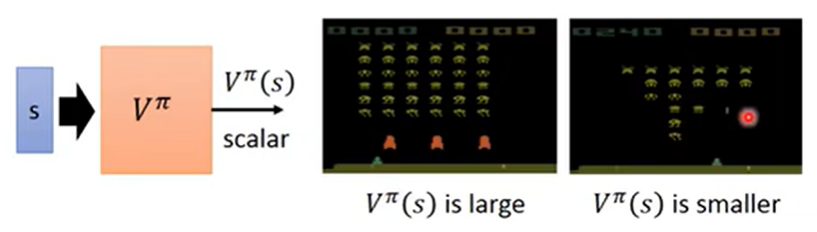
例如上图，剩下的怪不多了的时候，$V^{\pi}(s)$ 就会比较小；反之，剩下的怪多的时候，$V^{\pi}(s)$ 就会比较大。

这里注意：critic 是必须要绑定一个 actor 的。critic 没办法凭空去评估一个状态的好坏；它评估的东西是给定一个状态，假设接下来跟环境互动的 actor 是 $\pi$，那么会得到多少奖励。因为就算给同一个状态，给定不同的 $\pi$，得到的奖励也会不一样的。（譬如很叼的玩家会在绝境秀操作，很捞的玩家就只会是个呆头鹅）

所以 critic 的取值跟状态和 actor 都有关。critic 是用来衡量某一个 actor 的好坏，而不是去一般化地衡量某一个状态的好坏。

如何估计 critic $V^\pi(s)$

方法一：蒙特卡洛方法（Monte-Carlo approach, MC）

critic 看到 actor $\pi$ 在玩游戏。

• 假设观察到状态 $s_a$：到这一句游戏结束，累积奖励为 $G_a$
• 假设观察到状态 $s_b$：到这一句游戏结束，累积奖励为 $G_b$
• 那么希望 $V^\pi(s_a)$ 与 $G_a$ 越接近越好，$V^\pi(s_b)$ 与 $G_b$ 越接近越好
• 这就是一个回归问题

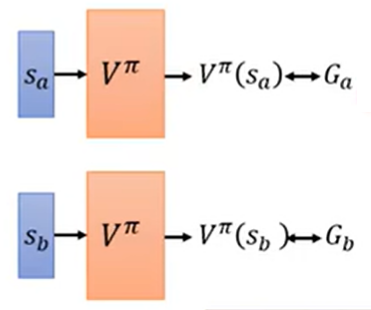
要把游戏都玩到底，才能看到累积奖励 $G_a, G_b, \ldots$ 是什么。

方法二：时序差分方法（Temporal Difference approach, TD）

critic 看到 actor $\pi$ 在玩游戏。

• 看到 actor 在状态 $s_t$ 的时候采取动作 $a_t$，状态跳到 $s_{t+1}$，得到奖励 $r_t$
• $V^\pi(s_t)=V^\pi(s_{t+1}) + r_t$
• 具体训练如下图：让 $V^\pi(s_t)-V^\pi(s_{t+1})$ 与 $r_t$ 越接近越好

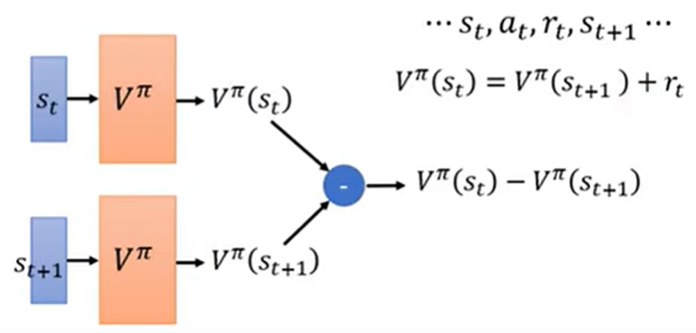
好处：可以不玩完游戏就能开始更新网络参数（可能在某些情况下玩完一把游戏耗时太久）

MC 和 TD 的差别

MC 会具有较大方差 累积奖励 $G_a$ 可以被是为一个随机变量。同样走到状态 $s_a$ 的时候，由于游戏本身和策略都具有随机性，$G_a$ 是不一样的。注意到累积奖励 $G_a$ 是多步奖励之和。把某一个变量乘上 $k$ 倍的话，注意到方差的性质：$Var[k X] = k^2 Var[X]$，所以此时方差就会变成 $k^2$ 倍。下面的图，上面是 MC，下面是 TD。TD 每次只拟合一个 $r$，而 MC 是把所有的 $r$ 给累积起来拟合。

TD 不见得估得准 V 如果 $V^{\pi}(s_{t+1})$ 估得不准的话，那么 $V^{\pi}(s_{t})$ 也会跟着估得不准。

TD 应用较常见，MC 较少应用。

例子 下面这个例子，MC 和 TD 会得出不同的 $V^{\pi}(s_a)$ 值。哪一个对？其实都对。

• 在第一个轨迹中，$s_a$ 得到奖励 0，跳到 $s_b$，得到奖励为 0
• 一个可能是 $s_a$ 就是一个霉比状态。只要看到 $s_a$ 之后，在 $s_b$ 就拿不到奖励。也就是说，状态 $s_a$ 会影响 $s_b$
• 另一个可能是看到了 $s_a$ 之后看到 $s_b$ 只是一个巧合。只是因为单纯运气的问题，平常看到 $s_b$ 得到的奖励是 3/4，只不过在第一个轨迹那次恰好看到 $s_b$ 得到的奖励为 0
• 不同的方法，可能考虑到不同的假设，所以会得到不同的运算结果

上面说的 critic 函数在应用策略 $\pi$ 时，对状态进行评估，形式为 $V^{\pi}(s)$；还有一种 critic 函数，对状态和动作均进行评估，形式为 $Q^{\pi}(s, a)$，称为 Q 函数（Q function）。

$Q^{\pi}(s, a)$ 的含义就是当 actor 采取 $\pi$ 的时候，在状态 $s$ 时采取动作 $a$ 后，得到的 期望累积奖励。

有一个非常重要的一点：actor 采取 $\pi$ 的时候，在看到状态 $s$ 时所采取的动作不一定是 $a$！譬如 actor 可以是一个神经网络，此时看到一个状态 $s$ 之后采取的动作是一个概率分布。$Q^{\pi}(s, a)$ 考虑的是 actor 在见到状态 $s$ 之后，强制采取动作 $a$，接下来都用 $\pi$ 继续玩下去。也就是说，只有在状态为 $s$ 时才强制采取动作 $a$，之后让 $\pi$ 接管，自动把游戏玩下去，得到期望累积奖励。

Q 函数有两种写法：一种是输入状态 $s$ 和动作 $a$，得到一个 $Q^{\pi}(s, a)$ 的值；另一种更常用的是输入状态 $s$，假设动作 $a$ 是离散的，Q 函数直接吐出所有动作 $a$ 的对应 $Q^{\pi}(s, a)$。

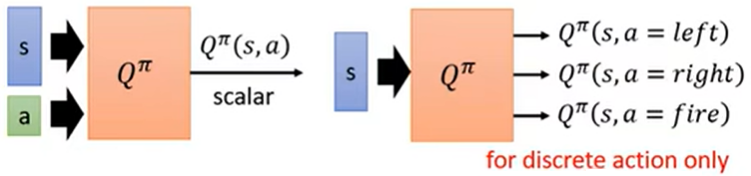
Q-learning：另一种使用 Critic 的方式

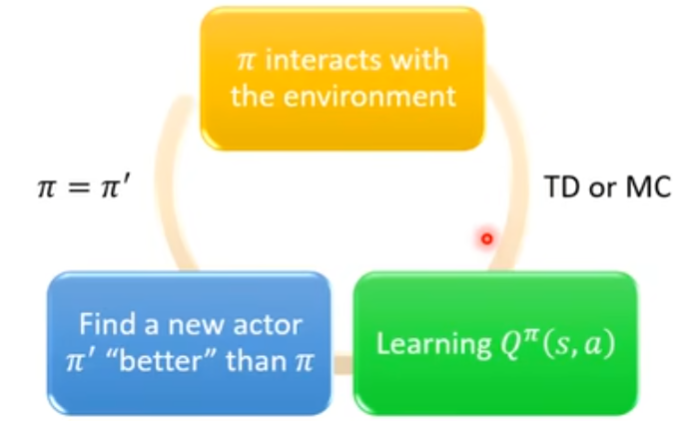
实际上，只要有了 Q 函数，我们就能做强化学习！（采取哪一种动作）

• 假设初始的 actor 叫作 $\pi$，它与环境互动会得到数据
• 衡量 $\pi$ 在某个状态强制采用哪个动作，接下来用 $\pi$ 能得到的累积奖励，即 $\pi$ 这个 actor 的 Q 值
• 只要学得出 $\pi$ 的 Q 函数，那么就可以得到一个新的策略 $\pi’$，这个 $\pi’$ 就会比原来的策略 $\pi$ 要好 (什么叫作“好”？)
• 把原来的 $\pi$ 替代为 $\pi’$，一直循环下去，策略就会越来越好

什么叫作“好”？ 对于所有（同一）状态 $s$ 而言，$\pi$ 的 value 一定会不大于 $\pi’$ 的 value，即

$$V^{\pi'}(s) \ge V^{\pi}(s)$$

这个性质通过 $\pi’$ 的更新式而确定：

$$\pi'(s) = \arg \max_{a} Q^{\pi}(s, a)$$

对于离散情况，可以这样理解：在某个状态 $s$ 的时候，把每个可能的动作 $a$ 都带入到 $Q^{\pi}$ 中，看看哪个动作 $a$ 对应的 Q 函数 $Q^{\pi}(s, a)$ 取值最大。这一个动作 $a$ 就是 actor $\pi’$ 会采取的动作。

但是，给定状态 $s$，actor $\pi$ 并不一定会采取动作 $a$。Q 函数的定义是让 $\pi$ 在看到状态 $s$ 时，强制采取状态 $a$ 的累积奖励。

所以，没有一个所谓的策略叫作 $\pi’$，$\pi’$ 其实就是用 Q 函数推出来的。

对于状态 $a$ 是连续的情况，这里先留个坑

为什么会更“好”？ 这里给出 $V^{\pi’}(s) \ge V^{\pi’}(s)$ 的证明。

根据 Q 函数的定义：$V^{\pi}(s)$ 为 $\pi$ 在看到状态 $s$ 之后的累积奖励，而 $\pi$ 在看到状态 $s$ 后会采取动作 $\pi(s)$：

$V^{\pi}(s) = Q^{\pi}(s, \pi(s))$

这个 Q 值肯定不大于 actor $\pi$ 在看到状态 $s$ 之后，把所有动作 $a$ 都枚举一遍，取得的最大 Q 值：

$V^{\pi}(s) = Q^{\pi}(s, \pi(s)) \le \max_{a} Q^{\pi}(s, a)$

由于 $\pi’(s) = \arg \max_{a} Q^{\pi}(s, a)$，因此 $\max_{a} Q^{\pi}(s, a)$ 又可以写作 $Q^{\pi}(s, \pi’(s))$

所以连起来，就是 $V^{\pi}(s) \le Q^{\pi}(s, \pi’(s))$

也就是说，在看到状态 $s$ 之后，如果按照 actor $\pi$ 来作决策，那么得到的奖励一定会不大于，现在这个状态 $s$ 时故意不按照 actor $\pi$ 指示的决策，而是按照 $\pi’$ 的决策采取动作，但是接下来的动作都按照 $\pi$ 的指示来做。也就是说，“一步之差”所得到的累积奖励比完全按照 $\pi$ 所得到的累积奖励还可能要更大。

然后就是总结起来：如果每一步都是按照 $\pi’$ 来做决策，而不是按照 $\pi$ 的话，所得到的累积奖励也会要大于等于之前的累计误差的，所以就可以串起来（用数学式子写出来）：

$$\begin{aligned}V^{\pi}(s) &\le Q^{\pi}(s, \pi'(s)) \\ &=\mathbb{E}[r_t + V^{\pi}(s_{t+1}) | s_t = s, a_t = \pi'(s_t)] \\ &\le \mathbb{E}[r_t + Q^{\pi}(s_{t+1}, \pi'(s_{t+1})) | s_t = s, a_t = \pi'(s_t)] \\ &=\mathbb{E}[r_t + r_{t+1} + V^{\pi}(s_{t+2}) | \ldots] \\ &\le \mathbb{E}[r_t + r_{t+1} + Q^{\pi}(s_{t+2}, \pi'(s_{t+2})) | \ldots] \\ &\le \ldots \le V^{\pi'}(s)\end{aligned}$$

(最要耐烦的其实是这一步，也就是说要展开出期望式)

• 取期望值：每一次取 $(s_t, a_t)$ 所得到的奖励 $r_t$ 和下一步状态 $s_{t+1}$ 不见得是一样的
• 然后又可以将不等式 $V^{\pi}(s) \le Q^{\pi}(s, \pi’(s))$ 应用到 $V^{\pi}(s_{t+1})$ 里面

Target Network

在学习 Q 函数的时候，也会用到 TD 的概念。

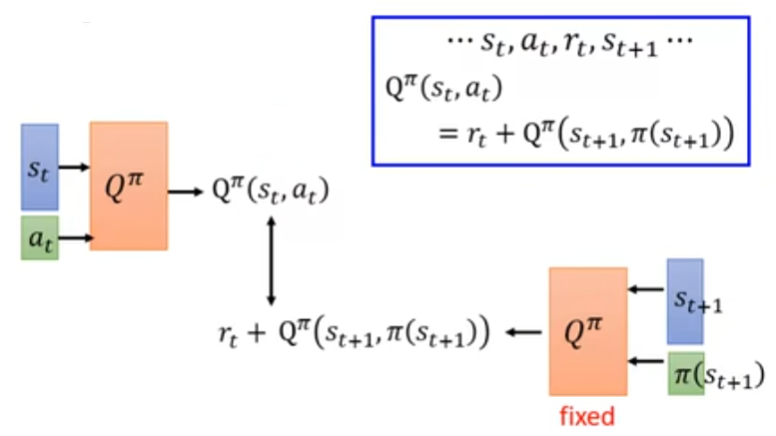
假设收集到数据：收集到状态 $s_t$，在该状态的时候采取动作 $a_t$，并且得到奖励 $r_t$，以及看到下一步状态 $s_{t+1}$，那么根据 Q 函数的定义：

$$Q^{\pi}(s_{t}, a_{t}) = r_t + Q^{\pi}(s_{t+1}, \pi(s_{t+1}))$$

希望在 $(s_{t}, a_{t})$ 时候的 Q 值和在 $(s_{t+1}, \pi(s_{t+1}))$ 时候的 Q 值，它们的差应该是 $r_t$。所以这里就借鉴 TD 的思想，设计了这样的一个训练流程。

但是这么一般的函数是不好学的：如果把它看成一个回归问题的话，回归目标是一直在动的。这样一来，训练就会不太稳定。所以在实操的时候，往往会把其中一个网络给固定下来：一般选下面这个网络。网络固定之后，下面这个回归的目标就也会是固定的。只调左边的网络参数，就是一个可以把 MSE 作为 loss 的回归问题。

在左边的网络参数更新 N 次后（譬如 100 次），再用左边网络参数去替换掉右边的网络参数（copy），来进行更新。

（两边不要一起动，一起动结果就会坏掉）

loss 会不会变成 0？其实不太会，因为两边输入的 $(s, a)$ 不一样，而且下面还加了个 $r_t$。

Exploration

策略基于 Q 函数：$a = \arg \max_{a} Q(s, a)$。

这和策略梯度不一样：

• 在做策略梯度的时候，我们的输出是随机的，也就是说每次学习到的是采取动作的概率分布，每次会在这个分布里面采样，得到具体的动作
• 而上述的函数形式所得出的动作是确定的：这不是一个好的收集数据的方式。一定要在状态 $s$ 的时候采取动作 $a$ 之后，才能估出 $Q(s, a)$；换言之，假设没有采取到动作 $a$，$Q(s, a)$ 是估不出的。（这个问题尤其对于查表式策略，对于深度网络式的 Q 可能会好那么一丢丢）具体看下面的图解：

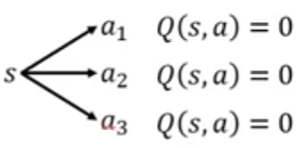
• 在初始情形，每个动作都没被访问到，所以每个动作的 Q 值都是一个初始值，譬如 0

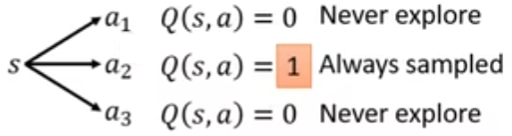
• 然后，通过对 $a_2$ 的采样，$Q(s, a_2)$ 的值被更新成一个正值
• 由策略式，我们在看到状态 $s$ 时总会采取动作 $a_2$，此时其他的策略都不会被采样到。这样，模型就永远不知道其他动作的 Q 值是多少。

有两个解决这个问题的方法：

Epsilon Greedy 将策略改写成：

$$a = \left\{ \begin{aligned}\arg\max_{a} Q(s, a), & \qquad \textrm{with probability } 1 - \varepsilon \\ \textrm{random}, & \qquad \textrm{otherwise}\end{aligned} \right.$$

譬如，将 $\varepsilon$ 设为 0.1，那么策略有 0.9 的概率选取最优动作，有 0.1 的概率探索其他动作。

一般而言，$\varepsilon$ 应随学习的进程而减小：一开始可能我们会花很多精力去探索不同的动作；随着训练次数越来越多，已经确定哪些动作是比较好的，我们就会减少探索，把 $\varepsilon$ 的值变小（这里的设计可以参考模拟退火）

Boltzmann Exploration 这里就有点像策略梯度：策略梯度里面网络的输出是一个由 softmax 产生的各动作的概率分布。这里类似，可以根据 $Q(s, a)$ 的值来做一个基于 softmax 产生的概率分布：

$$P(a | s) = \frac{\exp(Q(s, a))}{\sum_{a}\exp(Q(s, a))}$$

假设某一个动作 $a$，它的 Q 值 $Q(s, a)$ 越大，就代表这个动作越好，采取它的概率就越大；反之，如果有一个动作 $a$ 的 Q 值 $Q(s, a)$ 较小，不代表我们不能试试看这个动作 $a$，看看它究竟好不好用。

因为 Q 值有正有负，所以用 softmax 来产生概率分布。

（在训练的开始，随机化的 Q 值可能会造成这个分布趋向于均匀分布）

Replay Buffer

现在会有一个策略 $\pi$ 跟环境做互动，收集训练数据。将这些训练数据都存到一个 buffer 里面，buffer 里面每一条数据都是一个经验，包含 $(s_t, a_t, r_t, s_{t+1})$，这里并不需要采样整个轨迹。

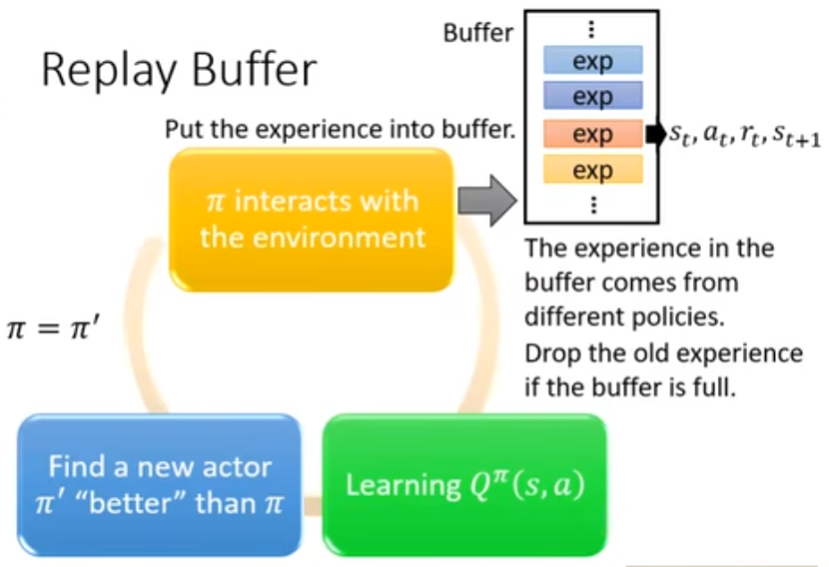
注意这个 buffer 里面的数据可能来自于不同的策略。如果 buffer 满了，就把最旧的数据给丢掉。

有了这个 buffer 以后，训练过程变成：

1. 随机从这个 buffer 里面挑一个 batch 的数据
2. 根据这个 batch 的数据，更新 Q 函数

当我们这样做的时候，变成了一个 off-policy 的做法：我们更新的时候，是更新在 actor $\pi$ 下的 Q 函数，但是数据来源不全是来源于 $\pi$。这样，我们减少了跟环境做互动的次数，而且 batch 内的数据更多样化

但是我们在关注 $\pi$ 的 Q 函数的时候，引入了一大堆别的 actor 所产生的数据来做更新，有没有关系？

其实是没有关系的。这并不一定是因为过去的 $\pi$ 和现在的 $\pi$ 很像。个人理解是，如果过去的 $\pi$ 和现在的 $\pi$ 不像的话，那么过去的 $a_t$ 跟现在的 $a_t$ 可能也不太像，这就引入了现在 $\pi$ 可能不那么关注的其他的动作的结果，增加了多样化。

Q-learning 的算法流程总结

1. 初始化 Q 函数 $Q$，设目标 Q 函数 $\hat{Q} = Q$。
2. 在每个 episode：拿 agent 跟环境去互动。对于每一步 $t$：
   1. 给定状态 $s_t$，基于现在的 $Q$，采用探索机制（epsilon greedy，Boltzmann exploration），采取动作 $a_t$
   2. 得到奖励 $r_t$，得到新的状态 $s_{t+1}$。至此得到了一个数据 $(s_t, a_t, r_t, s_{t+1})$
   3. 将这个数据 $(s_t, a_t, r_t, s_{t+1})$ 丢到 buffer 里面（如果 buffer 满了，就把最旧的一个数据丢掉）
   4. 从 buffer 中采样 一批 数据 $(s_i, a_i, r_i, s_{i+1})$（刚才放进去的数据可能没被采样到）
   5. 回归目标 $y = r_i + \max_{a}{\hat{Q}(s_{i+1}, a)}$（回归目标要用目标网络 $\hat{Q}$ 来算）
   6. 更新 $Q$ 的参数，以使 $Q(s_i, a_i)$ 的值尽可能靠近 $y$（回归问题）
   7. 每 $C$ 次重设 $\hat{Q}$ 的参数 $\hat{Q} = Q$