李宏毅强化学习个人笔记 - PPO

• 回到概览

PPO: Proximal Policy Optimization，该算法为 OpenAI 的默认强化学习算法。

复习：将神经网络作为 actor

• 神经网络擅长拟合函数
• 网络输入：机器的观测表示成向量或矩阵；
• 网络输出：每个动作对应输出层的一个神经元；

$p(s_{t+1}|s_t, a_t)$ 不能控制，由环境来决定，我们只能控制 $p_{\theta}(a_t|s_t)$。

任务是要最大化期望累积奖励 $\bar{R}_{\theta}$

$$\bar{R}_{\theta}=\sum_{\tau}R(\tau) p_{\theta}(\tau)=E_{\tau \sim p_{\theta}(\tau)}[R(\tau)]$$

（注意到 $R_{\theta}$ 是一个随机变量）

也就是说，在 $p_{\theta}(\tau)$ 这个分布里面采样轨迹 $\tau$，计算 $R(\tau)$ 的期望值。

然后 $R(\tau)$ 这一项不需要可微。上一次讲到策略梯度（Policy Gradient）可以推出：

$$\begin{align*}\nabla \bar{R}_{\theta} & \approx \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_n}{R(\tau^n) \nabla \log p(a_t^n|s_t^n,\theta)}\end{align*}$$

这样就需要拿 actor $\pi_{\theta}$ 和环境互动，采集数据，得到游戏记录。

在一般分类问题的实现基础上分别乘以每个轨迹的累积奖励 $R(\tau)$。

1. 加一个 baseline（偏置）：前面提过的“如果都是正奖励……”
2. 给每一个动作一个合适的得分（对累积奖励的贡献应合理）。
   • “游戏玩了之后的结果是好的，不代表每一步都是对的”
   • 理想状况下，能通过较多次的采样解决这个问题（多个结果就能暴露某一步的错误）；但是现实不可能采样那么多次
   • 不计算整场游戏的奖励，而是计算当前步的累积奖励。
   • 当前操作到游戏结束是一个“subgame”，一个操作的 subgame 的奖励分数是对这个操作的更好评价
   • 而且还可以加一个衰减因子 $\gamma$：跟当前的步数越远，影响越小

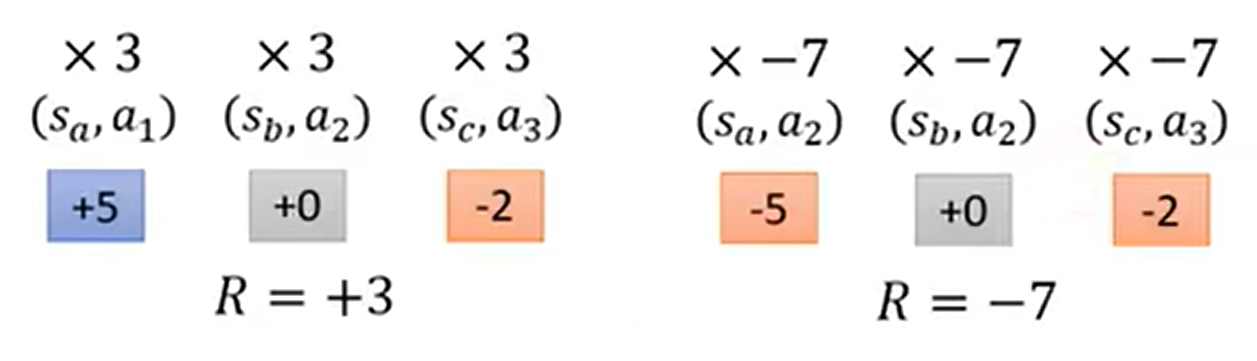
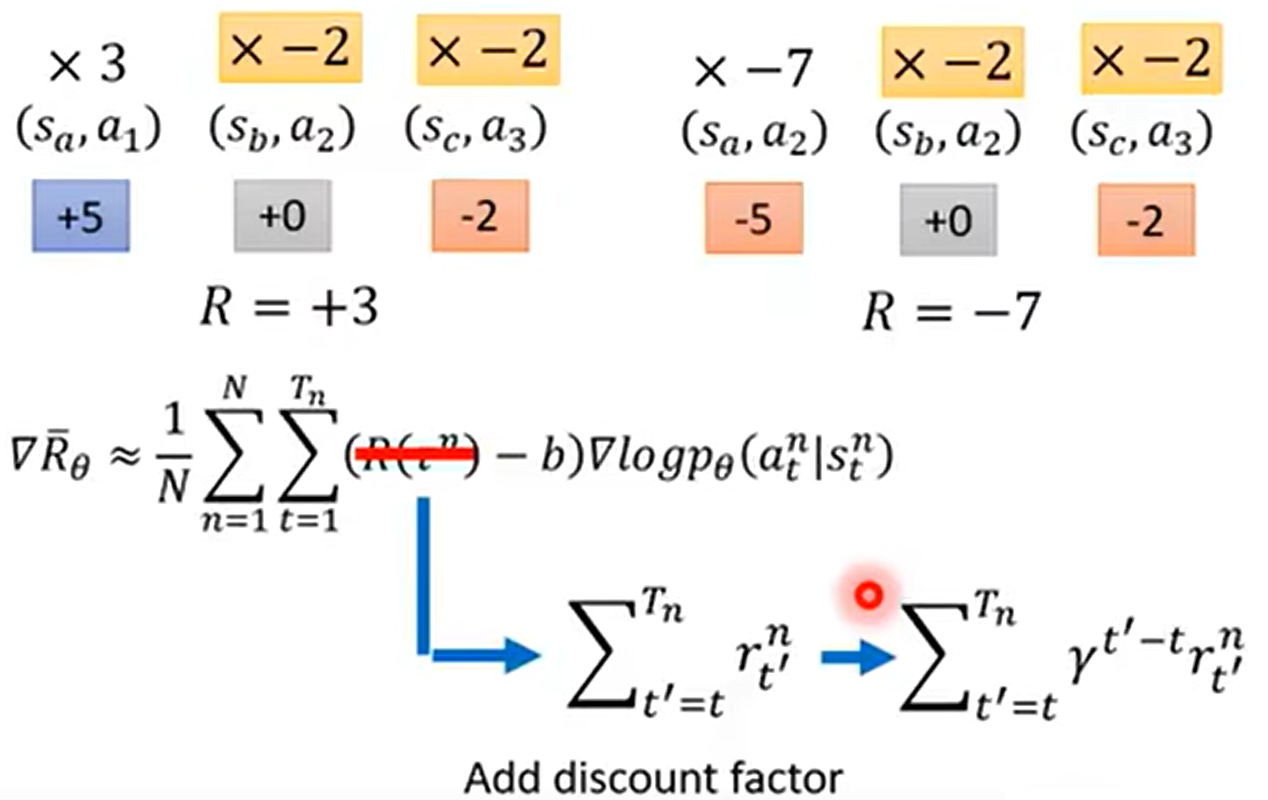
然后 $R(\tau^n)-b$ 这一项可以拿出来，叫成 Advantage Function $A^{\theta}(s_t, a_t)$：如果我们在状态 $s_t$ 时采用动作 $a_t$，相较于其他动作，能够有多好。

$A^{\theta}(s_t, a_t)$ 可以被 critic 估计出来。

On-policy → Off-policy：不止一次地用到与环境交互的经验

• On-policy：智能体学到的与智能体与环境交互的经验相同；
• Off-policy：智能体学到的与智能体与环境交互的经验不同；

这也就是 PPO 中“proximal”近似一词的来源。

• 自己下棋：on-policy
• 别人下棋，自己在旁边看：off-policy

On-policy 的做法

$$\nabla \bar{R}_{\theta}=E_{\tau \sim p_{\theta}(\tau)}[R(\tau) \nabla \log p_{\theta}(\tau)]$$

这里，我们用 $\pi_\theta$ 来和环境互动，收集数据。更新 $\theta$ 时，我们不得不再次采样，获得训练数据。（因为 $\theta$ 更新之后，$p_{\theta}(\tau)$ 这个概率就不对了，之前采样的数据就不能用了）

所以，我们想用另外一个固定的参数 $\theta’$，用基于此参数的 actor $\pi_{\theta’}$ 跟环境做互动，这样我们就能复用之前采样到的训练数据。

重要性采样（Importance Sampling）

该方法也可以被用在 RL 之外的领域中。

假设有一个 $f(x)$。要想计算 $E_{x \sim p}[f(x)]$，但是没有办法直接对 $p$ 这个分布做积分。

• 可以从 $p$ 这个分布里面采样出一些样本 $x^i$，则有 $E_{x \sim p}[f(x)] \approx 1/N \sum_{i=1}^{N}{f(x^i)}$
• 现如今，我们没办法从 $p(x)$ 这个分布里面采样出样本，但是可以从另外一个分布 $q(x)$ 里面采样出样本 $x^i$，其中 $q$ 几乎可以是任意的分布。
• 那么此时算期望就没办法直接套用上面那个采样的近似式
• 所以就尝试做一个修正（嗯凑）

$$\begin{aligned} E_{x \sim p}[f(x)] &= \int f(x) p(x) \mathrm{d} x \\ &=\int f(x) \frac{p(x)}{q(x)} q(x) \mathrm{d} x \\ &= E_{x \sim q}\left [f(x) \frac{p(x)}{q(x)}\right] \end{aligned}$$

这样就把“从 $p$ 里面采样算期望值”变成了“从 $q$ 里面采样算期望值”。因为分布被改变了，所以需要乘上一个修正项 $p(x) / q(x)$。（只是说 $q(x) = 0$ 的时候如果 $p(x) \ne 0$ 的话就会爆掉。换言之 $q(x) = 0$ 的时候，$p(x)$ 也应为 $0$）

实操中的问题：两分布 $p$ 和 $q$ 不能差太大

这是因为，如果我们算方差，而非期望：

$$Var_{x \sim p}[f(x)]$$

和

$$Var_{x \sim q}\left[f(x) \frac{p(x)}{q(x)}\right]$$

是不一样的。（两随机变量的均值一样，但是方差不见得是一样的）

注意到方差的计算公式：

$$Var[X] = E[X^2] - (E[X])^2$$

把这个公式往上面的式里面一代入：

$$Var_{x \sim p}[f(x)] = E_{x \sim p}[f(x)^2] - (E_{x \sim p}[f(x)])^2$$ $$Var_{x \sim q}\left[f(x) \frac{p(x)}{q(x)}\right] = E_{x \sim q}\left[f(x)^2 \frac{p(x)^2}{q(x)^2}\right] - \left(E_{x \sim q}\left[f(x) \frac{p(x)}{q(x)}\right]\right)^2$$

把这个式子用上面嗯凑的方法凑回去，凑成 $x \sim p$ 形式的期望，有：

$$Var_{x \sim q}\left[f(x) \frac{p(x)}{q(x)}\right] = E_{x \sim p}\left[f(x)^2 \frac{p(x)}{q(x)}\right] - \left(E_{x \sim p}\left[f(x) \right]\right)^2$$

两项的不一样就体现在第一项中，后者比前者多了一个 $p(x)/q(x)$。如果分布 $p$ 和 $q$ 差太大的话，随机变量的方差就会差很多。这时，如果采样的样本数不够多的话，那么差别就会比较大。

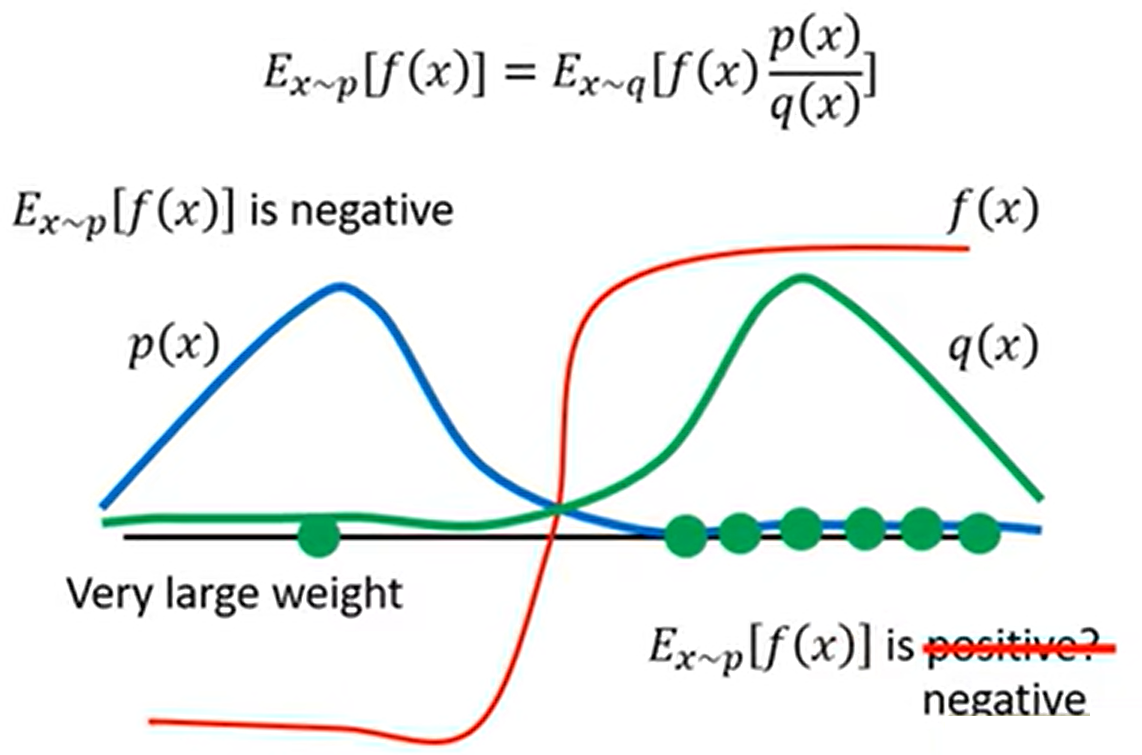
当分布 $p$ 和 $q$ 差距较大的时候，如上图所示：

• 我们在 $x \sim p$ 的时候总会采样到 $f(x)$ 为负的点，算出来的期望为负的。
• 如果我们把分布从 $p$ 换到 $q$ 的话，我们总会采样到 $f(x)$ 为正的点，算出来的期望为正的。

强化学习的算法从 On-policy 迁移到 Off-policy

回顾之前的 On-policy 算法：

$$\nabla \bar{R}_{\theta}=E_{\tau \sim p_{\theta}(\tau)}[R(\tau) \nabla \log p_{\theta}(\tau)]$$

现在到 Off-policy 之后：

$$\nabla \bar{R}_{\theta}=E_{\tau \sim p_{\theta'}(\tau)}\left[\frac{p_{\theta}(\tau)}{p_{\theta'}(\tau)} R(\tau) \nabla \log p_{\theta}(\tau)\right]$$

可以把 $\theta$ 换成另外一个 $\theta’$，不过求的期望内容要补上一个 weight 修正。

也就是说：

• 用参数为 $\theta’$ 的 actor 进行采样；
• 用采样得到的数据多次训练 $\theta$。

回顾之前，我们实际上可能不把一局游戏玩完，也就是得不到一整个轨迹 $\tau$。也就是说，通过把 $\nabla \log p_\theta(\tau)$ 乘开之后，可以把更新化成这样：

$$\nabla \bar{R}_{\theta} = E_{(s_t, a_t) \sim \pi_\theta}\left[A^{\theta}(s_t, a_t) \nabla \log p_\theta(a_t^n | s_t^n)\right]$$

用 $\theta$ 采样出 $(s_t, a_t)$，并计算 advantage，也就是 $(s_t, a_t)$ 有多好。

$A^{\theta}(s_t, a_t)$ 是估测出来的，在状态 $s_t$ 时采取动作 $a_t$ 有多好。如果该项是正的，那么概率 $p_\theta(a_t^n | s_t^n)$ 需要增加；如果该项是负的，那么概率 $p_\theta(a_t^n | s_t^n)$ 需要减少。

现在把带有 advantage function 的上式化成 off-policy 的：

$$\begin{aligned}\nabla \bar{R}_{\theta} &= E_{(s_t, a_t) \sim \pi_\theta}\left[A^{\theta}(s_t, a_t) \nabla \log p_\theta(a_t^n | s_t^n)\right] \\ &= E_{(s_t, a_t) \sim \pi_{\theta'}}\left [\frac{P^{\theta}(s_t, a_t)}{P^{\theta'}(s_t, a_t)} A^{\theta}(s_t, a_t) \nabla \log p_\theta(a_t^n | s_t^n)\right]\end{aligned}$$

变换方式（推导过程）跟之前的化成积分式“硬凑”的方法一致。

上式的 $A^{\theta}(s_t, a_t)$ 在我们将参数 $\theta$ 换成 $\theta’$ 的时候，应该改成 $\theta’$，也就是说上式应该写成：

$$\nabla \bar{R}_{\theta} = E_{(s_t, a_t) \sim \pi_{\theta'}}\left[\frac{P^{\theta}(s_t, a_t)}{P^{\theta'}(s_t, a_t)} {\color{red}A^{\theta'}(s_t, a_t)} \nabla \log p_\theta(a_t^n | s_t^n)\right]$$

这是因为：

• $A$ 这一项是想要估测在某一个状态 $s_t$ 采取某一个动作 $a_t$，接下来会得到累计奖励的值减掉 baseline。
• 之前是 $\theta$ 在跟环境做互动，所以这里观察到的是 $\theta$ 得到的奖励；
• 现在是 $\theta’$ 在跟环境做互动，所以这里得到的 advantage 其实是根据 $\theta’$ 估测出来的。
• 先假设这两项 $A^{\theta}(s_t, a_t)$ 和 $A^{\theta’}(s_t, a_t)$ 是差不多的

然后进一步将联合概率 $P^{\theta}(s_t, a_t)$ 拆解成条件概率 $p^{\theta}(a_t | s_t) p^{\theta}(s_t)$ 之后，上式变为：

$$\nabla \bar{R}_{\theta} = E_{(s_t, a_t) \sim \pi_{\theta'}}\left[\frac{p^{\theta}(a_t | s_t)}{p^{\theta'}(a_t | s_t)}\frac{p^{\theta}(s_t)}{p^{\theta'}(s_t)} A^{\theta'}(s_t, a_t) \nabla \log p_\theta(a_t^n | s_t^n)\right]$$

然后假设模型在参数为 $\theta$ 时看到状态 $s_t$ 的概率 $p^{\theta}(s_t)$，和在参数为 $\theta’$ 时看到状态 $s_t$ 的概率 $p^{\theta’}(s_t)$ 是 近似相等 的。可以找个理由：

• 看到什么状态往往跟采取什么动作往往是没什么关系的；
• 实际上这一项 $p^{\theta}(s_t)$ 根本就 不太可能去算……拿参数为 $\theta$ 的模型跟环境互动，太难算出 $p^{\theta}(s_t)$ 了；
• 但是算条件概率 $p^{\theta}(a_t | s_t)$ 是不难的：只需要把状态 $s_t$ 代入到模型的网络中，模型就会吐出在状态 $s_t$ 时会采取动作 $a_t$ 的概率 $p^{\theta}(a_t | s_t)$。

所以上式就变成这样：

$$\nabla \bar{R}_{\theta} = E_{(s_t, a_t) \sim \pi_{\theta'}}\left[\frac{p^{\theta}(a_t | s_t)}{p^{\theta'}(a_t | s_t)} A^{\theta'}(s_t, a_t) \nabla \log p_\theta(a_t^n | s_t^n)\right]$$

从梯度反推回原来的目标函数：

$$J^{\theta'}(\theta) = E_{(s_t, a_t) \sim \pi_{\theta'}}\left[\frac{p^{\theta}(a_t | s_t)}{p^{\theta'}(a_t | s_t)} A^{\theta'}(s_t, a_t) \right]$$

这个反推需要注意到公式：$\nabla f(x) = f(x) \nabla \log f(x)$

把 $p_{\theta}(a_t | s_t)$ 当作是 $f(x)$，跟上面的分母合起来就变成 $\nabla p_{\theta}(a_t | s_t)$，也就是

$$\nabla J^{\theta'}(\theta) = E_{(s_t, a_t) \sim \pi_{\theta'}}\left[\frac{\nabla p^{\theta}(a_t | s_t)}{p^{\theta'}(a_t | s_t)} A^{\theta'}(s_t, a_t) \right]$$

要还原求梯度之前的样子，也就是还原出 $J^{\theta’}(\theta)$ 的形式，也就是把右侧的梯度算子 $\nabla$ 给拿掉即可。

上面这个 $J^{\theta’}(\theta)$ 符号的含义：

• 括号里面的 $\theta$ 表示我们需要优化的参数
• 上标的 $\theta’$ 是说我们用 $\theta’$ 去跟环境互动，采样出 $(s_t, a_t)$
• 我们得到 $(s_t, a_t)$ 之后，计算出 advantage $A^{\theta’}(s_t, a_t)$，然后再乘上概率的商
• 多次互动取期望
• （这里留了一个坑：如此更新，何时终止？）

这样，我们就能用 off-policy 来替换 on-policy。

PPO / TRPO

回顾之前我们说到我们从一个概率分布变到另一个分布的时候，可以利用重要性采样的手法。但是这两个分布不能差太多。如何避免两分布差太多的问题？

PPO 的优化式如下：

$$J_{\mathrm{PPO}}^{\theta'}(\theta) = J^{\theta'}(\theta) - \beta \mathrm{KL}(\theta, \theta')$$

也就是说，在训练的时候加一个限制，使得和环境互动的 $\theta’$ 与更新的参数 $\theta$ 差别不要太大。该限制为 $\theta$ 和 $\theta’$ 的 KL 散度，像一个正则化一样，也就是说让 $\theta$ 与 $\theta’$ 越像越好。

PPO 的前身 TRPO 的优化式如下：

$$\begin{aligned}J_{\mathrm{TRPO}}^{\theta'}(\theta) =& J^{\theta'}(\theta), \\ s.t. \quad &\mathrm{KL}(\theta, \theta') < \delta\end{aligned}$$

也就是说，对 KL 散度的限制所放的位置不一样。

• PPO 直接把 KL 散度丢到了优化式里面，直接利用梯度上升即可训练。
• TRPO 把 KL 散度当成一个限制，希望小于一个值 $\delta$，比较难处理。
• PPO 和 TRPO 实际效果差不多，但是 PPO 实现起来简单多了。
• 当然也可以理解为凸优化中把限制转换到优化式中的技巧之类的，譬如拉格朗日乘数法。

何为 KL 散度？这里并不是说把 $\theta$ 和 $\theta’$ 当成两个分布，去算参数上的距离；而是算 这两个参数下行为的距离。也就是说，给定同样的状态的时候，这两个参数给出的动作（两个概率分布）的差异。

有可能参数变了很多，但是实际上 actor 的行为差异很小。

PPO 算法流程如下：

1. 初始化策略参数 $\theta^0$
2. 在每轮迭代中：
   1. 用 $\theta^k$ 来跟环境交互，从而采样到状态和动作 $(s_t, a_t)$，以及计算 advantage $A^{\theta^k}(s_t, a_t)$
   2. 用 $J_{\mathrm{PPO}}(\theta)$ 来优化 $\theta$： $$J_{\mathrm{PPO}}^{\theta^k}(\theta) = J^{\theta^k}(\theta) - \beta \mathrm{KL}(\theta, \theta^k)$$
   3. 更新很多次的参数 $\theta$
   4. 如果 $\mathrm{KL}(\theta, \theta’) > \mathrm{KL}_{\max}$，则增大 $\beta$ 的值
   5. 如果 $\mathrm{KL}(\theta, \theta’) < \mathrm{KL}_{\min}$，则减小 $\beta$ 的值

其中上面的 4.和 5.是自适应动态调整参数 $\beta$（自适应 KL 惩罚项），需要设置能接受的最大 KL 散度 $\mathrm{KL}_{\max}$ 和最小 KL 散度 $\mathrm{KL}_{\min}$。d.表示 KL 散度的惩罚没太发挥作用；e.表示 KL 散度的惩罚太强了，影响了对目标函数 $J^{\theta^k}(\theta)$ 的优化。

PPO2

PPO 的加强版。PPO2 的整个目标函数如下：

$$J_{\mathrm{PPO2}}^{\theta^k}(\theta) \approx \sum_{(s_t, a_t)} \min\left(\frac{p^{\theta}(a_t | s_t)}{p^{\theta^k}(a_t | s_t)} A^{\theta^k}(s_t, a_t), \mathrm{clip}\left(\frac{p^{\theta}(a_t | s_t)}{p^{\theta^k}(a_t | s_t)}, 1-\varepsilon, 1+\varepsilon\right) A^{\theta^k}(s_t, a_t) \right)$$

• 首先是对 $(s_t, a_t)$ 中两项较小的求和
• $\varepsilon$ 是一个需要调的超参数
• 第一项就是 PPO 中的 $J^{\theta^k}(\theta)$
• 第二项先把两个概率之商限制到 $(1 - \varepsilon, 1 + \varepsilon)$ 之内
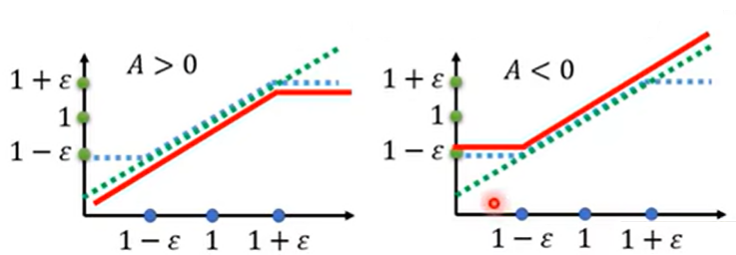
• 见下图，分为 $A > 0$ 和 $A < 0$ 两种情形，横轴为 $p^{\theta}(a_t | s_t) / p^{\theta^k}(a_t | s_t)$，第一项对应绿色的线，第二项对应蓝色的线，取较小之后变成红色的线
• 希望 $p^{\theta}$ 和 $p^{\theta^k}$ 不要差距太大
• 如果 $A > 0$，也就是说某个状态和动作 $(s_t, a_t)$ 是好的。我们想要把 $(s_t, a_t)$ 出现的概率调大，也就是说让 $p^{\theta}$ 越大越好；但是 $p^{\theta}$ 和 $p^{\theta^k}$ 的比值不应超过 $1 + \varepsilon$。如果超过了，就没有收益了
• 反之，如果 $A < 0$，希望把 $(s_t, a_t)$ 出现的概率调小，但是小到 $p^{\theta}$ 和 $p^{\theta^k}$ 的比值不超过 $1 - \varepsilon$