这里我们不学习 actor，也就是不学习怎么做事，而是学习一个 critic。

critic 的性质

  • critic 本身不决定动作；
  • 给定 actor，critic 可以评估 actor 的好坏；
  • 实际上，可以从 critic 里面得到一个 actor，这就是 Q-learning。
  • critic 实际上就是一个评估 actor $\pi$ 的函数 $V^\pi$
    • 这个函数可以是一个神经网络

critic 的形式

关于状态 $V^\pi(s)$ 当 actor 使用 $\pi$ 的时候，在观测到状态 $s$ 后获得的期望累积奖励。

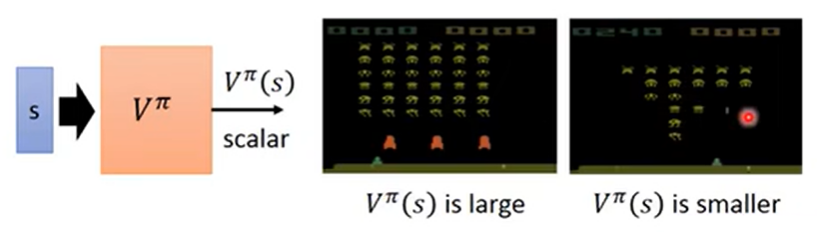
如上图：

  • 左边的状态，还剩很多飞机可以打，所以 $V^\pi(s)$ 较大；
  • 右边的状态，较少飞机可以打，而且飞机渐渐靠下了，所以 $V^\pi(s)$ 较小。

对于不同的 actor $\pi$，给出一样的状态，可能给出的 critic $V^\pi(s)$ 也会不同。

  • 譬如棋魂中的例子，之前藤原佐为建议进藤光下小飞，因为之前进藤光比较弱，后续变化较简单，更易驾驭；
  • 之后变强了，就能够下变化更复杂的大飞；
  • 也就是说，critic 会随着不同的 actor 得到不同的分数。

如何估计 critic $V^\pi(s)$

方法一：蒙特卡洛方法（Monte-Carlo approach, MC）

critic 看到 actor $\pi$ 在玩游戏。

  • 假设观察到状态 $s_a$：到这一句游戏结束，累积奖励为 $G_a$
  • 假设观察到状态 $s_b$：到这一句游戏结束，累积奖励为 $G_b$
  • 那么希望 $V^\pi(s_a)$ 与 $G_a$ 越接近越好，$V^\pi(s_b)$ 与 $G_b$ 越接近越好

方法二：时序差分方法（Temporal Difference approach, TD）

critic 看到 actor $\pi$ 在玩游戏。

  • 看到 actor 在状态 $s_t$ 的时候采取动作 $a_t$，状态跳到 $s_{t+1}$，得到奖励 $r_t$
  • $V^\pi(s_t)=V^\pi(s_{t+1}) + r_t$
  • 具体训练如下图：让 $V^\pi(s_t)-V^\pi(s_{t+1})$ 与 $r_t$ 越接近越好

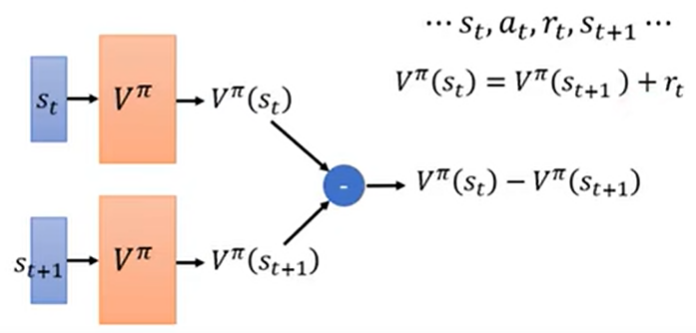
好处：可以不玩完游戏就能开始更新网络参数（可能在某些情况下玩完一把游戏耗时太久）

关于状态和动作 $Q^\pi(s, a)$ 当 actor 使用 $\pi$ 的时候，在观测到状态 $s$ 以及采取动作 $a$ 后获得的期望累积奖励。

指定状态，不同动作采取的奖励可能不同。

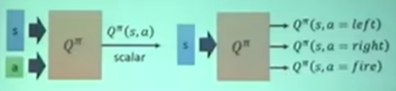
上图右边画出了动作 $a$ 可以被穷举的情况。

Q-Learning 概览

  • 有一个初始的 actor $\pi$
  • 让 actor $\pi$ 与环境互动，通过 TD 或者 MC 学到 Q-function（估出 critic）
  • 找到一个新的 actor $\pi’$，它比 $\pi$ 要更好
  • 更新 $\pi$ 为 $\pi’$，循环操作。

给定 $Q^\pi(s, a)$，如何找到一个比 $\pi$ 更好的 $\pi’$

“更好”的定义：对于所有可能的状态 $s$，$V^{\pi’}(s) \ge V^{\pi}(s)$（用 $\pi’$ 玩游戏得到的奖励都不小于用 $\pi$ 玩游戏得到的奖励）

寻找方法：

给定状态 $s$，穷举所有可能的动作 $a$，看看哪个 Q-value $Q^{\pi}(s, a)$ 最大。Q 之前看过 $\pi$ 做过的事情，所以知道在状态 $s$ 时采取动作 $a$ 的奖励。

  • $\pi’$ 没有额外的参数，其仅依赖于 $Q$
  • 不太适合连续的动作 $a$

用 TD 来估计 $Q^{\pi}(s, a)$

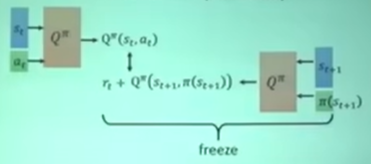
奇技淫巧

Google rainbow 这篇 paper。

包含 Double DQN 和 Dueling DQN。