李宏毅强化学习个人笔记 - 基于策略的方法（学习actor）

• 回到概览

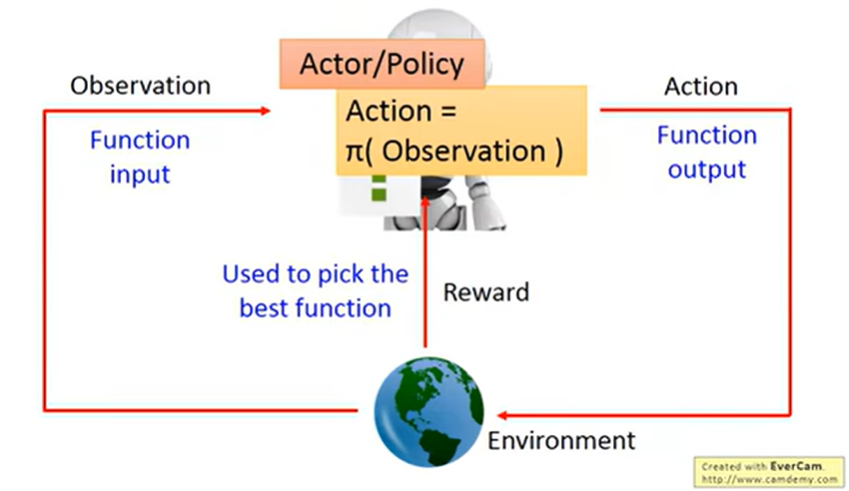
基于策略的方法，也就是学习 actor。换言之，也就是学习一个策略函数 $\pi$：该函数输入观测，输出动作。

一图流

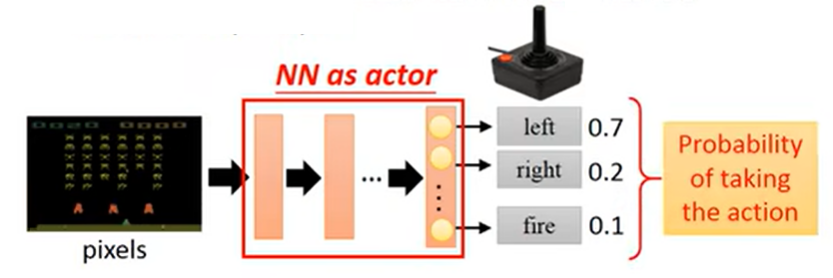
将神经网络作为 actor

• 神经网络擅长拟合函数
• 网络输入：机器的观测表示成向量或矩阵；
• 网络输出：每个动作对应输出层的一个神经元；

一图流

神经网络相较于查表的作为 actor 的好处

• 有“采样”的步骤，可以带来更多变的决策。譬如猜拳，会随机出锤子剪刀布。

• 譬如上面的打飞机，无法穷举所有的像素值，这种情况下建立表不现实。

• 神经网络泛化性好，可以举一反三。就算有些画面机器完全没有看过，也能够得到较好的结果（动作）。

决定 actor 的好坏

回顾监督学习：用 loss 来刻画所学到函数的质量。

• 求网络参数 ${\theta }^{\prime }$ 使得能够最小化总误差 $L$
• 或者说，使得预测分布与目标（target）越近越好

给定具有网络参数 $\theta$ 的 actor：${\pi }_{\theta }(s)$，用该 actor 来玩游戏：

• 每一步可以记为三元组：(观测, 动作, 奖励)
• $(s_1,a_1,r_1)\to (s_2,a_2,r_2)\to \dots \to (s_T,a_T,r_T)$
• 总奖励：$R_{\theta }=\sum _{t=1}^T{r}_t$
• 不是要优化某一步的奖励，而是要优化总的奖励
• 就算用同样的参数 $\theta$，得到的奖励也会不同
  • 由于 actor 的动作是通过采样得到的，所以具有一定随机性
  • 环境本身也会具有随机性
  • 故而，$R_{\theta }$ 为一个随机变量
  • 记 ${\overline{R}}_{\theta }$ 为 $R_{\theta }$ 的期望，该期望值衡量了 actor（${\pi }_{\theta }$）的好坏。希望该期望越大越好
• 一局游戏（episode）可被视为轨迹（trajectory）$\tau$
  • $\tau =\{s_1,a_1,r_1,s_2,a_2,r_2,\dots ,s_T,a_T,r_T\}$
  • 此时可将总奖励记为 $R(\tau )=\sum _{t=1}^T{r}_t$
  • 只选择一个 actor 来玩游戏的话，纵使可能的结果会有许多种，但是最后只会看到一种游戏结果（只被采样到一个）
    • 每个轨迹可能被采样的概率由 actor 的参数 $\theta$：$P(\tau |\theta )$（为什么这里用大写的 P？因为 注意到 $\tau$ 是一个随机变量）
    • 有些游戏场景会较常出现，有些场景会较少出现。
    • 此时累积奖励的期望可被写为 ${\overline{R}}_{\theta }=\sum _{\tau }R(\tau )P(\tau |\theta )$
    • 也就是对所有游戏的可能 $\tau$ 求期望
    • 当然穷举所有的 $\tau$ 不可能，所以一般是用 actor ${\pi }_{\theta }$ 玩 $n$ 次游戏，得到 $n$ 个不同的轨迹 $\{{\tau }^1,{\tau }^2,\dots ,{\tau }^N\}$，也就是说从 $P(\tau |\theta )$ 中采样 $N$ 次（采样出的 $\tau$ 次数与概率成正比）
    • 也就是说，${\overline{R}}_{\theta }=\sum _{\tau }R(\tau )P(\tau |\theta )\approx 1/N\sum _{n=1}^{N}R({\tau }^n)$

选一个最好的函数（actor）

问题描述：

找参数 ${\theta }^{\ast }=\arg \underset{\theta }{max}{\overline{R}}_{\theta }$

其中 ${\overline{R}}_{\theta }$ 为累积奖励的期望，定义遵循上文 ${\overline{R}}_{\theta }=\sum _{\tau }R(\tau )P(\tau |\theta )$

方法：梯度上升（由于求的是最大化）

$${\theta }^k\leftarrow {\theta }^{k-1}+\eta \mathrm{\nabla }{\overline{R}}_{{\theta }^{k-1}}$$

譬如，假设 $\theta$ 的参数为 $w_1,w_2,\dots ,b_1,\dots$，那么 ${\overline{R}}_{\theta }$ 的偏微分 $\mathrm{\nabla }{\overline{R}}_{\theta }$ 就是

$$\mathrm{\nabla }{\overline{R}}_{\theta }=\left[\begin{array}{c}\partial {\overline{R}}_{\theta }/\partial w_1\\ \partial {\overline{R}}_{\theta }/\partial w_2\\ ⋮\\ \partial {\overline{R}}_{\theta }/\partial b_1\\ ⋮\end{array}\right]$$

梯度上升的实际计算

由于

$${\overline{R}}_{\theta }=\sum _{\tau }R(\tau )P(\tau |\theta )$$

那么

$$\mathrm{\nabla }{\overline{R}}_{\theta }=\sum _{\tau }R(\tau )\mathrm{\nabla }P(\tau |\theta )$$

由此可见：累积奖励 $R(\tau )$ 不需要是可微的，甚至可以是一个黑盒。

再者，$R(\tau )$ 是环境给我们的，我们有时会对 $R(\tau )$ 缺乏理解，譬如说打飞机里面可能会有一些随机性。

继续，让 $P(\tau |\theta )$ 嗯是要出现在外面：

$$\mathrm{\nabla }{\overline{R}}_{\theta }=\sum _{\tau }R(\tau )\mathrm{\nabla }P(\tau |\theta )=\sum _{\tau }R(\tau )P(\tau |\theta )\frac{\mathrm{\nabla }P(\tau |\theta )}{P(\tau |\theta )}$$

然后就能写成：

$$\mathrm{\nabla }{\overline{R}}_{\theta }=\sum _{\tau }R(\tau )P(\tau |\theta )\mathrm{\nabla }\log P(\tau |\theta )$$

然后因为看到了求和号为 $\sum _{\tau }$，求和里面有 $P(\tau |\theta )$ 这一项，所以就可以对 $\tau$ 采样进行近似（这也是我们上面在外面嗯凑出一个 $P(\tau |\theta )$ 的原因）。也就是说：

$$\mathrm{\nabla }{\overline{R}}_{\theta }\approx \frac{1}{N}\sum _{n=1}^{N}R({\tau }^n)\mathrm{\nabla }\log P({\tau }^n|\theta )$$

接下来的问题，就是如何计算梯度 $\mathrm{\nabla }\log P({\tau }^n|\theta )$。首先用条件概率公式展开：

$$P(\tau |\theta )=p(s_1)p(a_1|s_1,\theta )p(r_1,s_2|s_1,a_1)p(a_2|s_2,\theta )p(r_2,s_3|s_2,a_2)\dots$$

• 游戏的开局状态 $s_1$ 有可能不同
• 采取动作 $a_1$ 取决于开局状态 $s_1$ 和模型参数 $\theta$
• 采取动作 $a_1$ 后，环境跳到状态 $s_2$ 也有一个概率在这里，以及奖励 $r_1$ 也会具有一定随机性
• $p(s_1),p(r_1,s_2|s_1,a_1),p(r_2,s_3|s_2,a_2),\dots$ 与 actor 没关系
• $p(a_1|s_1,\theta ),p(a_2|s_2,\theta ),\dots$ 与 actor 有关系

$$P(\tau |\theta )=p(s_1)\prod _{t=1}^{T}p(a_t|s_t,\theta )p(r_t,s_{t+1}|s_t,a_t)$$

常用技巧：概率相乘→对数概率相加，这一点其实也因为我们恰好就需要算 $\log P(\tau |\theta )$

$$\log P(\tau |\theta )=\log p(s_1)+\sum _{t=1}^T\log p(a_t|s_t,\theta )+\log p(r_t,s_{t+1}|s_t,a_t)$$

又有因为我们求的是梯度 $\mathrm{\nabla }\log P({\tau }^n|\theta )$，所以我们可以干掉上式中的常数项，也就是表达式中没有出现 $\theta$ 的那些项

$$\mathrm{\nabla }\log P(\tau |\theta )=\sum _{t=1}^T\mathrm{\nabla }\log p(a_t|s_t,\theta )$$

也就是说，累积奖励期望的梯度 $\mathrm{\nabla }{\overline{R}}_{\theta }$ 可以被近似为

$$\begin{array}{rl}\mathrm{\nabla }{\overline{R}}_{\theta }& \approx \frac{1}{N}\sum _{n=1}^{N}R({\tau }^n)\mathrm{\nabla }\log P({\tau }^n|\theta )\\ & =\frac{1}{N}\sum _{n=1}^{N}R({\tau }^n)\sum _{t=1}^{T_n}\mathrm{\nabla }\log p(a_t^n|s_t^n,\theta )\\ & =\frac{1}{N}\sum _{n=1}^N\sum _{t=1}^{T_n}R({\tau }^n)\mathrm{\nabla }\log p(a_t^n|s_t^n,\theta )\end{array}$$

上式就是大名鼎鼎的 策略梯度（policy gradient）。

上面公式的意义

• 和深度学习中的一样，这里我们习惯用下标表示 单个样本中某个值在序列中的标号，用上标表示 样本的标号
• $R({\tau }^n)$：在第 $n$ 次游戏的轨迹中所得到的累积奖励
• $\mathrm{\nabla }\log p(a_t|s_t,\theta )$：看到 $s_t$ 产生 $a_t$ 的概率的对数梯度
• 假设在第 $n$ 次玩游戏的过程中产生了轨迹 ${\tau }^n$，看到状态 $s_t^n$ 时采取动作 $a_t^n$，最后导致累积奖励 $R({\tau }^n)$ 为正的，那么我们就会调 $\theta$ 使得 $p(a_t^n|s_t^n,\theta )$ 变大；
• 反之，如果最后导致累积奖励 $R({\tau }^n)$ 为负的，那么我们就会调 $\theta$ 使得 $p(a_t^n|s_t^n,\theta )$ 变小；
• 上面考虑整个轨迹 ${\tau }^n$ 的累积奖励 $R({\tau }^n)$，而非单步的立即奖励 $r_t^n$，这点十分重要（假设仅考虑单步的立即奖励的话，那么譬如像打飞机，只会调大打飞机这个动作，而不会调大挪位置的动作）

为什么要对概率取 log

$$\mathrm{\nabla }\log p(a_t^n|s_t^n,\theta )=\frac{\mathrm{\nabla }p(a_t^n|s_t^n,\theta )}{p(a_t^n|s_t^n,\theta )}$$

假设能在某些轨迹 $\tau$ 中看到一个状态 $s$ 出现（随机的）。对于这个状态，actor 采取不同的动作，譬如：

• 1 次采取 a 这个动作，得到奖励为 2；
• 3 次采取 b 这个动作，得到奖励为 1。

在更新参数的时候，我们训练出来的 actor 偏好出现次数比较多的，即使那个动作并没有比较好。

譬如去调高 b，actor 的表现也未必好到哪里去；而因为 a 出现得太罕见，所以要最大化的东西对目标的影响也小。

这个时候，除掉概率就能够消除采样频率不同而造成更新有偏好的影响。

为什么奖励不能都为正

打飞机里面确实有可能出现这种情况。

在理想情况下确实不会出现问题。出现概率大的和小的一起增加，最后由于概率要对预测取 softmax，所以大的会增加比较小，小的会增加比较大。

但是实际上，我们做的是采样，也就是只会采到部分动作。

举到的一个例子

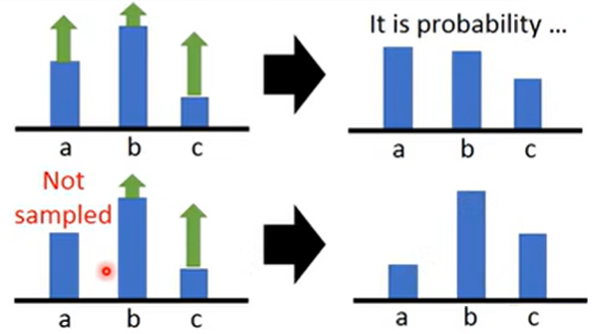
譬如上例中，我们只采样到 b 和 c。

这个时候，我们只会去调高这部分动作的，而 a 的动作没有被采样到，不知道它的 $R(\tau )$ 是多少。然后更新 actor 的时候，我们只会去拉高 b 和 c 的概率，这时 a 的概率就变得更低了，在接下来的与环境互动中 a 更少可能被采样到。

所以希望 $R(\tau )$ 有正有负：统一减掉一个 bias，让它有正有负。

$$\mathrm{\nabla }{\overline{R}}_{\theta }\approx \frac{1}{N}\sum _{n=1}^N\sum _{t=1}^{T_n}(R({\tau }^n)-b)\mathrm{\nabla }\log p(a_t^n|s_t^n,\theta )$$

实操

给定 actor 的参数 $\theta$，收集到若干数据（轨迹）：

• ${\tau }^1:(s_1^1,a_1^1)\to R({\tau }^1),(s_2^1,a_2^1)\to R({\tau }^1),\dots$
• ${\tau }^2:(s_1^2,a_1^2)\to R({\tau }^2),(s_2^2,a_2^2)\to R({\tau }^2),\dots$
• $\dots$

然后利用策略梯度与梯度上升更新参数，然后继续用更新后的参数去玩游戏……

但是 $\mathrm{\nabla }\log p(a_t^n|s_t^n,\theta )$ 的具体含义是什么？

回顾分类问题

一个栗子

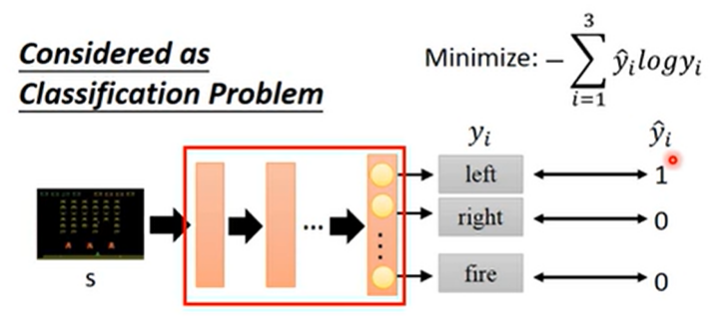
这里分类标签都是 one-hot 的，除了一个是 1，其他都是 0。要最小化

$$-\sum _{i=1}^3{\hat{y}}_i\log y_i$$

所以实际上就是在最大化 $\log y_1=\log p(“\mathrm{left}”|s)$

所以更新的时候也就是在做

$$\theta \leftarrow \theta +\eta \mathrm{\nabla }\log p("\mathrm{left}"|s)$$

希望预测结果与目标越接近越好

回到策略梯度

式子就是

$$\mathrm{\nabla }{\overline{R}}_{\theta }\approx \frac{1}{N}\sum _{n=1}^N\sum _{t=1}^{T_n}R({\tau }^n)\mathrm{\nabla }\log p(a_t^n|s_t^n,\theta )$$

也就是说，现在采样出 $(s_1^1,a_1^1)$ 之后，如果 $R({\tau }^1)$ 为正，那么希望之后 actor 的动作跟 $(s_1^1,a_1^1)$ 越接近越好。

而且，接近程度根据累积奖励 $R({\tau }^1)$ 来决定。换言之，相当于把每个训练数据都乘以权重 $R({\tau }^n)$。

比较花时间：需要更新→采样→更新→采样→……